| (6 intermediate revisions by the same user not shown) | |||
| Line 20: | Line 20: | ||
<math>X(f) = rect(\frac{\pi f}{W}) = \left\{\begin{array}{ll}1, & \text{ if }|t|<\frac{W}{2\pi},\\ 0, & \text{else.}\end{array} \right. \ </math> | <math>X(f) = rect(\frac{\pi f}{W}) = \left\{\begin{array}{ll}1, & \text{ if }|t|<\frac{W}{2\pi},\\ 0, & \text{else.}\end{array} \right. \ </math> | ||
| − | |||
| − | |||
b) the Nyquist rate | b) the Nyquist rate | ||
| Line 36: | Line 34: | ||
X_s(f) = CTFT\{ x_s(t) \} &= X(f)*\frac{1}{T}\sum_{k=-\infty}^{\infty}\delta(f-\frac{k}{T}) \\ | X_s(f) = CTFT\{ x_s(t) \} &= X(f)*\frac{1}{T}\sum_{k=-\infty}^{\infty}\delta(f-\frac{k}{T}) \\ | ||
&= \frac{1}{T}\sum_{k=-\infty}^{\infty}X(f-\frac{k}{T}) \\ | &= \frac{1}{T}\sum_{k=-\infty}^{\infty}X(f-\frac{k}{T}) \\ | ||
| − | &= \frac{3W}{2\pi}\sum_{k=-\infty}^{\infty}X(f-\frac{3Wk}{2\pi}) | + | &= \frac{3W}{2\pi}\sum_{k=-\infty}^{\infty}X(f-\frac{3Wk}{2\pi}) \\ |
| + | &= \frac{3W}{2\pi}\sum_{k=-\infty}^{\infty}rect(\frac{\pi f}{W}-\frac{3k}{2}) \\ | ||
\end{align}</math> | \end{align}</math> | ||
| − | |||
| − | |||
d) | d) | ||
| Line 48: | Line 45: | ||
X_d(\omega)=DTFT\{ x[n] \} &= X_s(\frac{\omega}{2\pi T}) \\ | X_d(\omega)=DTFT\{ x[n] \} &= X_s(\frac{\omega}{2\pi T}) \\ | ||
&= \frac{5W}{2\pi}\sum_{k=-\infty}^{\infty}X(\frac{\omega}{2\pi T}-\frac{5Wk}{2\pi}) \\ | &= \frac{5W}{2\pi}\sum_{k=-\infty}^{\infty}X(\frac{\omega}{2\pi T}-\frac{5Wk}{2\pi}) \\ | ||
| − | &= \frac{5W}{2\pi}\sum_{k=-\infty}^{\infty}X(\frac{5W}{2\pi}(\frac{\omega}{2\pi}-k)) | + | &= \frac{5W}{2\pi}\sum_{k=-\infty}^{\infty}X(\frac{5W}{2\pi}(\frac{\omega}{2\pi}-k)) \\ |
| + | &= \frac{5W}{2\pi}\sum_{k=-\infty}^{\infty}rect(\frac{5\omega}{4\pi}-\frac{5k}{2}) \\ | ||
\end{align}</math> | \end{align}</math> | ||
| − | [[Image: | + | [[Image:HW3Q1fig1.jpg|900px]] |
| + | |||
| + | (2) <math>x(t) = cos(2000\pi t)</math> | ||
| + | |||
| + | a)Compute CTFT of <math>x(t)</math>. Instead of using CTFT formula, we solve it by using inverse CTFT and comparison. | ||
| + | |||
| + | <math>\begin{align} | ||
| + | x(t) &= \frac{e^{j2000\pi t}+e^{-j2000\pi t}}{2}\ (*)\\ | ||
| + | x(t) &= \int\limits_{-\infty}^{\infty}X(f)e^{j2\pi ft}df\ (**) | ||
| + | \end{align}</math> | ||
| + | |||
| + | By comparing (*) and (**) we have | ||
| + | |||
| + | <math>X(f) = \frac{1}{2}(\delta(f-1000)+\delta(f+1000))</math> | ||
| + | |||
| + | b) the Nyquist rate | ||
| + | |||
| + | <math>f_0=1000</math> | ||
| + | |||
| + | c) | ||
| + | |||
| + | <math>T=\frac{1}{3f_0}=\frac{1}{3000}</math> | ||
| + | |||
| + | <math>x_s(t) = comb_T(x(t)) = x(t)\sum_{k=-\infty}^{\infty}\delta(t-kT)</math> | ||
| + | |||
| + | <math>\begin{align} | ||
| + | X_s(f) = CTFT\{ x_s(t) \} &= X(f)*\frac{1}{T}\sum_{k=-\infty}^{\infty}\delta(f-\frac{k}{T}) \\ | ||
| + | &= \frac{1}{T}\sum_{k=-\infty}^{\infty}X(f-\frac{k}{T}) \\ | ||
| + | &= 3000\sum_{k=-\infty}^{\infty}X(f-3000k) \\ | ||
| + | &= 1500\sum_{k=-\infty}^{\infty}[\delta(f-1000-3000k)+\delta(f+1000-3000k)] | ||
| + | \end{align}</math> | ||
| + | |||
| + | d) | ||
| + | |||
| + | <math>T=\frac{1}{5f_0}=\frac{1}{5000}</math> | ||
| + | |||
| + | <math>\begin{align} | ||
| + | X_d(\omega)=DTFT\{ x[n] \} &= X_s(\frac{\omega}{2\pi T}) \\ | ||
| + | &= 5000\sum_{k=-\infty}^{\infty}X(\frac{\omega}{2\pi T}-5000k) \\ | ||
| + | &= 5000\sum_{k=-\infty}^{\infty}X(5000(\frac{\omega}{2\pi}-k)) \\ | ||
| + | &= 2500\sum_{k=-\infty}^{\infty}[\delta(5000(\frac{\omega}{2\pi}-k)-1000)+\delta(5000(\frac{\omega}{2\pi}-k)+1000)] \\ | ||
| + | &= 2500\cdot \frac{2\pi}{5000}\sum_{k=-\infty}^{\infty}[\delta(\omega - \frac{2\pi}{5}-2\pi k) + \delta(\omega + \frac{2\pi}{5}-2\pi k)] \\ | ||
| + | &= \pi \sum_{k=-\infty}^{\infty}[\delta(\omega - \frac{2\pi}{5}-2\pi k) + \delta(\omega + \frac{2\pi}{5}-2\pi k)] | ||
| + | \end{align}</math> | ||
| + | |||
| + | [[Image:HW3Q1fig2.jpg|900px]] | ||
| + | |||
---- | ---- | ||
Latest revision as of 06:16, 19 October 2011
Homework 1, ECE438, Fall 2011, Prof. Boutin
Question 1-5
(1) $ x(t)=\frac{sin(Wt)}{\pi t} $
a) Compute CTFT of $ x(t) $. Instead of using CTFT formula, we solve it by using inverse CTFT and comparison.
$ \begin{align} x(t) &= \frac{sin(Wt)}{\pi t} = \frac{e^{jWt}-e^{-jWt}}{2j\pi t}\ (*)\\ x(t) &= \int\limits_{-\infty}^{\infty}X(f)e^{j2\pi ft}df\ (**) \end{align} $
Since
$ \int\limits_{-\frac{W}{2\pi}}^{\frac{W}{2\pi}}1\cdot e^{j2\pi ft}df = \frac{e^{jWt}-e^{-jWt}}{2j\pi t} $
Therefore,
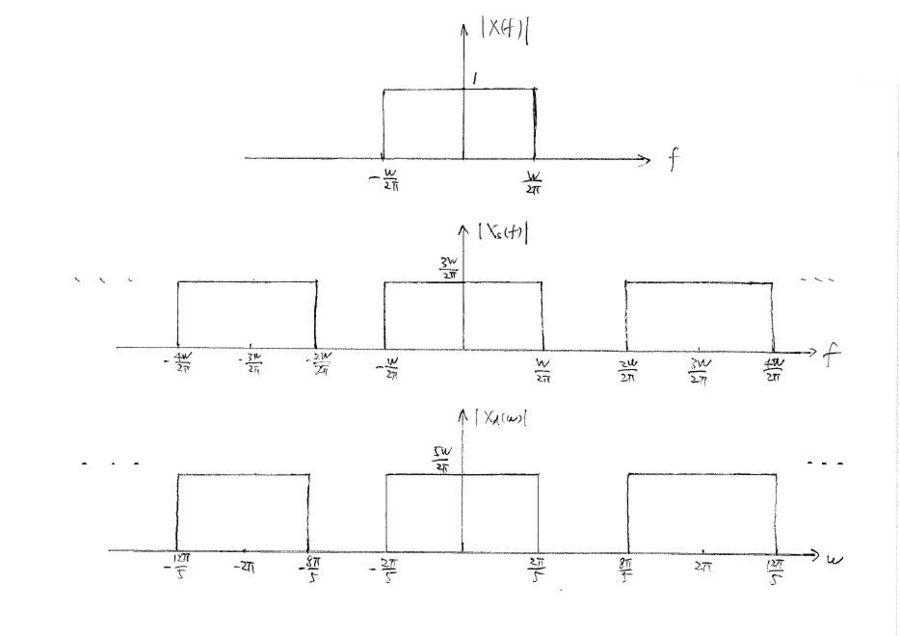
$ X(f) = rect(\frac{\pi f}{W}) = \left\{\begin{array}{ll}1, & \text{ if }|t|<\frac{W}{2\pi},\\ 0, & \text{else.}\end{array} \right. \ $
b) the Nyquist rate
$ f_0=\frac{W}{2\pi} $
c)
$ T=\frac{1}{3f_0}=\frac{2\pi}{3W} $
$ x_s(t) = comb_T(x(t)) = x(t)\sum_{k=-\infty}^{\infty}\delta(t-kT) $
$ \begin{align} X_s(f) = CTFT\{ x_s(t) \} &= X(f)*\frac{1}{T}\sum_{k=-\infty}^{\infty}\delta(f-\frac{k}{T}) \\ &= \frac{1}{T}\sum_{k=-\infty}^{\infty}X(f-\frac{k}{T}) \\ &= \frac{3W}{2\pi}\sum_{k=-\infty}^{\infty}X(f-\frac{3Wk}{2\pi}) \\ &= \frac{3W}{2\pi}\sum_{k=-\infty}^{\infty}rect(\frac{\pi f}{W}-\frac{3k}{2}) \\ \end{align} $
d)
$ T=\frac{1}{5f_0}=\frac{2\pi}{5W} $
$ \begin{align} X_d(\omega)=DTFT\{ x[n] \} &= X_s(\frac{\omega}{2\pi T}) \\ &= \frac{5W}{2\pi}\sum_{k=-\infty}^{\infty}X(\frac{\omega}{2\pi T}-\frac{5Wk}{2\pi}) \\ &= \frac{5W}{2\pi}\sum_{k=-\infty}^{\infty}X(\frac{5W}{2\pi}(\frac{\omega}{2\pi}-k)) \\ &= \frac{5W}{2\pi}\sum_{k=-\infty}^{\infty}rect(\frac{5\omega}{4\pi}-\frac{5k}{2}) \\ \end{align} $
(2) $ x(t) = cos(2000\pi t) $
a)Compute CTFT of $ x(t) $. Instead of using CTFT formula, we solve it by using inverse CTFT and comparison.
$ \begin{align} x(t) &= \frac{e^{j2000\pi t}+e^{-j2000\pi t}}{2}\ (*)\\ x(t) &= \int\limits_{-\infty}^{\infty}X(f)e^{j2\pi ft}df\ (**) \end{align} $
By comparing (*) and (**) we have
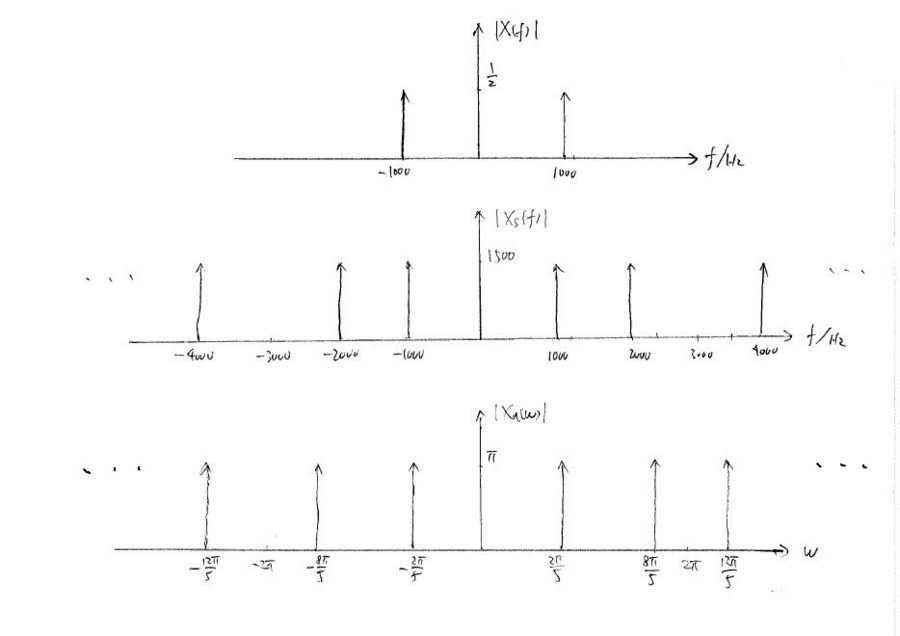
$ X(f) = \frac{1}{2}(\delta(f-1000)+\delta(f+1000)) $
b) the Nyquist rate
$ f_0=1000 $
c)
$ T=\frac{1}{3f_0}=\frac{1}{3000} $
$ x_s(t) = comb_T(x(t)) = x(t)\sum_{k=-\infty}^{\infty}\delta(t-kT) $
$ \begin{align} X_s(f) = CTFT\{ x_s(t) \} &= X(f)*\frac{1}{T}\sum_{k=-\infty}^{\infty}\delta(f-\frac{k}{T}) \\ &= \frac{1}{T}\sum_{k=-\infty}^{\infty}X(f-\frac{k}{T}) \\ &= 3000\sum_{k=-\infty}^{\infty}X(f-3000k) \\ &= 1500\sum_{k=-\infty}^{\infty}[\delta(f-1000-3000k)+\delta(f+1000-3000k)] \end{align} $
d)
$ T=\frac{1}{5f_0}=\frac{1}{5000} $
$ \begin{align} X_d(\omega)=DTFT\{ x[n] \} &= X_s(\frac{\omega}{2\pi T}) \\ &= 5000\sum_{k=-\infty}^{\infty}X(\frac{\omega}{2\pi T}-5000k) \\ &= 5000\sum_{k=-\infty}^{\infty}X(5000(\frac{\omega}{2\pi}-k)) \\ &= 2500\sum_{k=-\infty}^{\infty}[\delta(5000(\frac{\omega}{2\pi}-k)-1000)+\delta(5000(\frac{\omega}{2\pi}-k)+1000)] \\ &= 2500\cdot \frac{2\pi}{5000}\sum_{k=-\infty}^{\infty}[\delta(\omega - \frac{2\pi}{5}-2\pi k) + \delta(\omega + \frac{2\pi}{5}-2\pi k)] \\ &= \pi \sum_{k=-\infty}^{\infty}[\delta(\omega - \frac{2\pi}{5}-2\pi k) + \delta(\omega + \frac{2\pi}{5}-2\pi k)] \end{align} $
Question 6
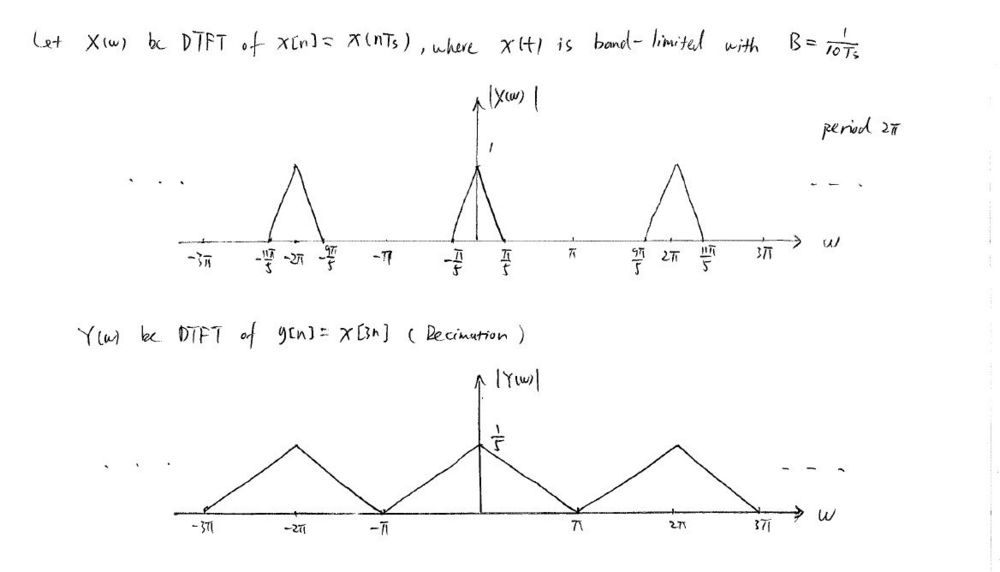
$ \text{a)} \;\; \text{General Relation for the decimation with a factor of } D \,\! $.
$ \text{Let } X(w) = \mathcal{F}(x[n]) $
$ \begin{align} Y(w) &= \sum_{n=-\infty}^{\infty} y[n]e^{-jwn} = \sum_{n=-\infty}^{\infty} x[3n]e^{-jwn} \\ &= \sum_{m=-\infty, m=Dk}^{\infty} x[m]e^{-j\frac{wm}{D}} = \sum_{m=-\infty}^{\infty} x[m] \left( \sum_{k=-\infty}^{\infty} \delta[m-Dk] \right) e^{-j\frac{wm}{D}} \\ &= \sum_{m=-\infty}^{\infty} x[m] \left( \frac{1}{D} \sum_{k=0}^{D-1} e^{j\frac{2\pi}{D}km} \right) e^{-j\frac{wm}{D}} = \sum_{k=0}^{D-1} \frac{1}{D} \sum_{m=-\infty}^{\infty} x[m]e^{j\left(w-\frac{2\pi}{D}k\right)m} \\ &= \sum_{k=0}^{D-1} \frac{1}{D} X\left(\frac{w-2\pi k}{D}\right) \\ \end{align} $
Replacing D with 5 would be the answer.
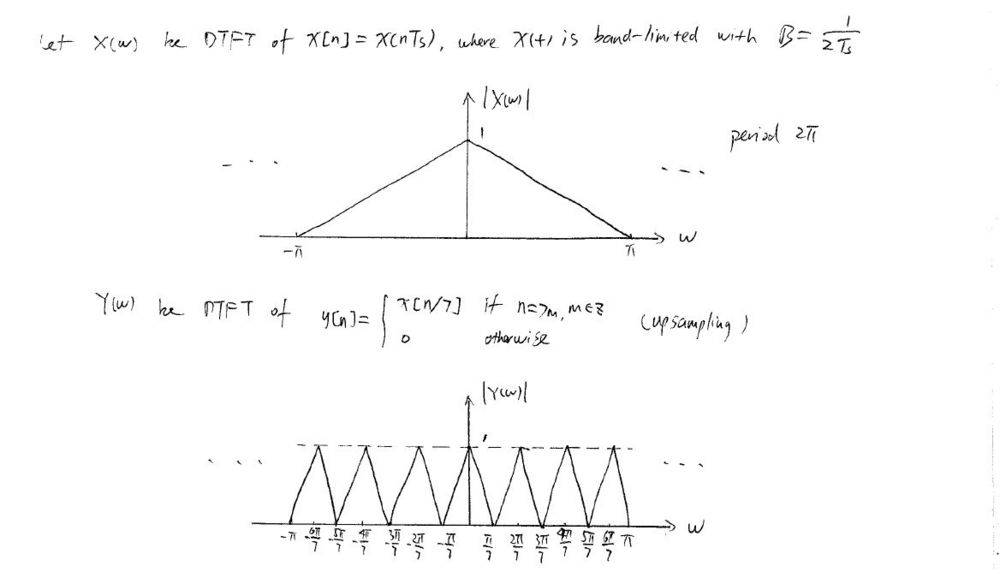
$ \text{b)} \;\; \text{General Relation for the upsampling with a factor of } L \,\! $.
$ \begin{align} Z(w) &= \sum_{n=-\infty}^{\infty} z[n]e^{-jwn} \\ &= \sum_{n=-\infty}^{\infty} \left( \sum_{k=-\infty}^{\infty} x[k] \delta[n-kL] \right) e^{-jwn} \\ &= \sum_{k=-\infty}^{\infty} x[k] \sum_{n=-\infty}^{\infty} \delta[n-kL] e^{-jwn} = \sum_{k=-\infty}^{\infty} x[k] e^{-jwkL} \\ &= \sum_{k=-\infty}^{\infty} x[k] e^{-jLwk} = X(Lw) \\ &\end{align} $
Since $ X(w) $ is periodic with $ 2\pi $, $ Z(w)=X(Lw) $ is periodic with $ 2\pi/L $.
Replaing L with 7 would be the answer.
Back to Homework 3
Back to ECE 438 Fall 2011