m |
|||
| (4 intermediate revisions by the same user not shown) | |||
| Line 3: | Line 3: | ||
---- | ---- | ||
| − | + | a. Note that systems g1 and g2 are Length-2 FIR filters which are of the form – | |
| − | + | ||
| − | + | ||
[[Image:Qp10q3fir.jpg|900px]] | [[Image:Qp10q3fir.jpg|900px]] | ||
| Line 11: | Line 9: | ||
<math> | <math> | ||
\begin{align} | \begin{align} | ||
| − | g1[n] &= | + | g1[n] &= a_1g1'[n] + b_1g1'[n-1] \\ |
| − | g2[n] &= | + | g2[n] &= a_1g2'[n] + b_1g2'[n-1] \\ |
\end{align} | \end{align} | ||
</math> | </math> | ||
| Line 20: | Line 18: | ||
<math> | <math> | ||
\begin{align} | \begin{align} | ||
| − | g1[n] &= a_1 | + | g1[n] &= a_1\delta[n] + b_1\delta[n-1] \\ |
| − | g2[n] &= a_2 | + | g2[n] &= a_2\delta[n] + b_2\delta[n-1]\\ |
\\ | \\ | ||
| Line 108: | Line 106: | ||
b. | b. | ||
| + | h[n] = h1[n] * g1[n] + h2[n] * g2[n] = <math>\delta[n-1]</math> <br/> | ||
| + | <math>H(\omega) = H1(\omega)G1(\omega) + H2(\omega)G2(\omega)</math> | ||
| + | Taking the Fourier transform, <br/> | ||
| + | <math> | ||
| + | \begin{align} | ||
| + | H(e^{j\omega}) &= (\frac{1}{2} + \frac{1}{2}e^{-j\omega}) (\frac{1}{2} + \frac{1}{2}e^{-j\omega}) + (\frac{1}{2} - \frac{1}{2}e^{-j\omega}) (-\frac{1}{2} + \frac{1}{2}e^{-j\omega}) \\ | ||
| + | &= (\frac{1}{2} + \frac{1}{2}e^{-j\omega})^2 - (\frac{1}{2} - \frac{1}{2}e^{-j\omega})^2 \\ | ||
| + | &= e^{-2j\omega /2}(\frac{e^{j\omega /2} + e^{-j\omega /2}}{2})^2 - | ||
| + | e^{-2j\omega /2}j^2(\frac{e^{j\omega /2} - e^{-j\omega /2}}{2j})^2 \\ | ||
| + | &= e^{-j\omega}cos^2(\omega /2) + e^{-j\omega}sin^2(\omega /2) \\ | ||
| + | &= e^{-j\omega} (cos^2(\omega /2) + sin^2(\omega /2)) \\ | ||
| + | &= e^{-j\omega} | ||
| + | \end{align} | ||
| + | </math> | ||
| + | Notice that by inverting H(<math>\omega</math>), we obtain h[n] = <math>\delta[n-1]</math> proving our answer in part a. | ||
| − | + | Taking the magnitude of the H(<math>\omega</math>),<br/> | |
| − | + | <math>|H(e^{jw})|</math> = 1 (Plot is line with constant value 1) <br/> | |
| + | Phase{<math>H(e^{jw}</math>)} = slope = -1 (Plot is line with slope -1 with value 0 at <math>\omega</math> = 0) | ||
Latest revision as of 03:31, 1 November 2010
Solution to Q3 of Week 10 Quiz Pool
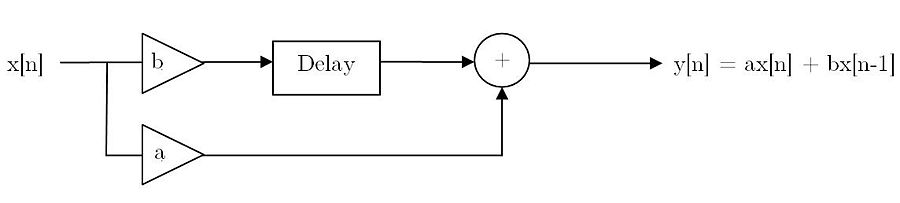
a. Note that systems g1 and g2 are Length-2 FIR filters which are of the form –
$ \begin{align} g1[n] &= a_1g1'[n] + b_1g1'[n-1] \\ g2[n] &= a_1g2'[n] + b_1g2'[n-1] \\ \end{align} $
or, looking at it in terms of impulse responses,
$ \begin{align} g1[n] &= a_1\delta[n] + b_1\delta[n-1] \\ g2[n] &= a_2\delta[n] + b_2\delta[n-1]\\ \\ \text{Given:} \\ g1[0] &= a_1 = (1/2) \\ \\ \text{To Find:} \\ g1[1] &= b_1 \\ g2[0] &= a_2 \\ g2[1] &= b_2 \\ \end{align} $
$ \begin{align} g1[n] = (1/2)\delta[n] + b_1\delta[n-1] \\ g2[n] = a_2\delta[n] + b_2\delta[n-1] \\ \end{align} $
$ \begin{align} G1(\omega) &= \frac{1}{2} + b_1z^{-1} \\ G2(\omega) &= a_2 + b_2z^{-1} \\ \end{align} $
It is also given to us that,
y[n] = x[n-1],
so feeding in $ \delta[n] $ as input (x[n]) would result in $ \delta[n-1] $.
Thus we require:
$ \begin{align} h1[n] * g1[n] + h2[n] * g2[n] &= \delta[n-1] \end{align} $
Taking Z transform,
$ \begin{align} H1(z)G1(z) + H2(z)G2(z) &= z^{-1} \\ \end{align} $
$ \begin{align} \frac{1}{2}(1+z^{-1})(\frac{1}{2} + b_1z^{-1}) + \frac{1}{2} (1- z^{-1}) (a_2 + b_2z^{-1}) &= z^{-1} \end{align} $
$ \begin{align} (1+z^{-1})(\frac{1}{2} + b_1z^{-1}) + (1- z^{-1}) (a_2 + b_2z^{-1}) &= 2z^{-1} \end{align} $
$ \begin{align} \frac{1}{2} + b_1z^{-1} + \frac{1}{2}z^{-1} + b_1z^{-2} + a_2 + b_2z^{-1} - a_2z^{-1} - b_2z^{-2} = 2z^{-1} \end{align} $
$ \begin{align} (\frac{1}{2} + a_2) + (\frac{1}{2} + b_1 + b_2 - a_2)z^{-1} + (b_1 - b_2)z^{-2} &= 2z^{-1} \end{align} $
Solve equation by equating coefficients of $ z^0, z^{-1}, z^{-2} $,
$ \frac{1}{2} + a_2 = 0, a_2 = -\frac{1}{2} $
$ \begin{align}b_1 - b_2 = 0, b_1 = b_2\end{align} $
$ \begin{align}\frac{1}{2} + b_1 + b_2 - a_2 = 2\end{align} $
$ \begin{align}\frac{1}{2} + 2b_1 + \frac{1}{2} = 2\end{align} $
$ \begin{align}2b_1 = 1, b_1 = \frac{1}{2}\end{align} $
$ \begin{align}b_2 = \frac{1}{2}\end{align} $
Therefore our two systems are -
$ \begin{align}g1[n] = \frac{1}{2}g1'[n] + \frac{1}{2}g1'[n-1]\end{align} $
$ \begin{align}g2[n] = -\frac{1}{2}g2'[n] + \frac{1}{2}g2'[n-1]\end{align} $
b.
h[n] = h1[n] * g1[n] + h2[n] * g2[n] = $ \delta[n-1] $
$ H(\omega) = H1(\omega)G1(\omega) + H2(\omega)G2(\omega) $
Taking the Fourier transform,
$ \begin{align} H(e^{j\omega}) &= (\frac{1}{2} + \frac{1}{2}e^{-j\omega}) (\frac{1}{2} + \frac{1}{2}e^{-j\omega}) + (\frac{1}{2} - \frac{1}{2}e^{-j\omega}) (-\frac{1}{2} + \frac{1}{2}e^{-j\omega}) \\ &= (\frac{1}{2} + \frac{1}{2}e^{-j\omega})^2 - (\frac{1}{2} - \frac{1}{2}e^{-j\omega})^2 \\ &= e^{-2j\omega /2}(\frac{e^{j\omega /2} + e^{-j\omega /2}}{2})^2 - e^{-2j\omega /2}j^2(\frac{e^{j\omega /2} - e^{-j\omega /2}}{2j})^2 \\ &= e^{-j\omega}cos^2(\omega /2) + e^{-j\omega}sin^2(\omega /2) \\ &= e^{-j\omega} (cos^2(\omega /2) + sin^2(\omega /2)) \\ &= e^{-j\omega} \end{align} $
Notice that by inverting H($ \omega $), we obtain h[n] = $ \delta[n-1] $ proving our answer in part a.
Taking the magnitude of the H($ \omega $),
$ |H(e^{jw})| $ = 1 (Plot is line with constant value 1)
Phase{$ H(e^{jw} $)} = slope = -1 (Plot is line with slope -1 with value 0 at $ \omega $ = 0)
Back to Lab Week 10 Quiz Pool
Back to ECE 438 Fall 2010 Lab Wiki Page
Back to ECE 438 Fall 2010