| Line 24: | Line 24: | ||
case 1: | case 1: | ||
| + | |||
[[Image:HW6_Q1_Case1.jpg]] | [[Image:HW6_Q1_Case1.jpg]] | ||
case 2: | case 2: | ||
| + | |||
[[Image:HW6_Q1_Case2.jpg|800px]] | [[Image:HW6_Q1_Case2.jpg|800px]] | ||
case 3: | case 3: | ||
| + | |||
[[Image:HW6_Q1_Case3.jpg]] | [[Image:HW6_Q1_Case3.jpg]] | ||
case 4: | case 4: | ||
| + | |||
[[Image:HW6_Q1_Case4.jpg|800px]] | [[Image:HW6_Q1_Case4.jpg|800px]] | ||
case 5: | case 5: | ||
| + | |||
[[Image:HW6_Q1_Case5.jpg|800px]] | [[Image:HW6_Q1_Case5.jpg|800px]] | ||
case 6: | case 6: | ||
| + | |||
[[Image:HW6_Q1_Case6.jpg|800px]] | [[Image:HW6_Q1_Case6.jpg|800px]] | ||
| Line 59: | Line 65: | ||
Q3. | Q3. | ||
| + | Denote N is the points number of the input signal's DFT. Then N=6. | ||
| + | |||
| + | 1) The normal DFT algorithm: If we use summation formula to compute DFT, according to the analysis of Q2. We need N*N=36 times of complex multiplications and N*(N-1)=30 times of complex additions. | ||
| + | |||
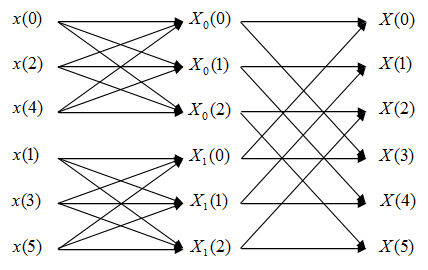
| + | Flow diagram of FFT: | ||
| + | |||
| + | [[Image:diagramFFT1.jpg]] | ||
| + | |||
| + | In this FFT algorithm, the computing of DFT is divided into two levels. First, we compute two 3 points DFT, which are DFT of even and odd points. | ||
| + | |||
| + | According to the analysis of Q2, we need N*N=9 times of complex multiplications and N*(N-1)=6 times of complex additions. Since we have to do this twice, we need 9*2=18 times of complex multiplications and 6*2=12 times of complex additions. | ||
| + | |||
| + | Second, we compute the final DFT by combing the first level result. According to the analysis of Q2, we need N/2=3 times of complex multiplications and N=6 times of complex additions. | ||
| + | |||
| + | In total, we need 18+3=21 times of complex multiplications and 12+6=18 times of complex additions. | ||
| + | |||
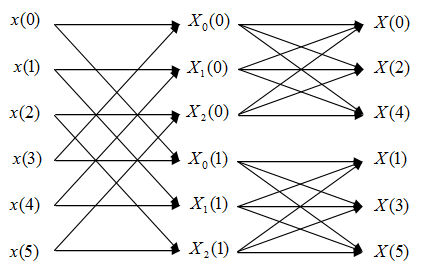
| + | 2) | ||
| + | |||
| + | [[Image:diagramFFT2.jpg]] | ||
| + | |||
| + | In this FFT algorithm, the computing of DFT is still divided into two levels. However, we will first compute three 2 points DFT, which are DFT of the first half points and the second half points. According to analysis of Q2, we need N/2=3 times of complex | ||
| + | multiplications and N=6 times of complex additions. | ||
| + | |||
| + | Second, we compute the two 3 points DFT using first level result. According to the analysis of Q2, for each 3 points DFT we need N*N=9 times of complex multiplications and N*(N-1)=6 times of complex additions. Since we have to do this twice, we need 9*2=18 times of complex multiplications and 6*2=12 times of complex additions. | ||
| + | |||
| + | In total, we need 3+18=21 times of complex multiplications and 6+12=18 times of complex additions. | ||
| + | Compare 1) and 2), both methods have the same amount of complex operations. | ||
------------------------------------ | ------------------------------------ | ||
Q4. | Q4. | ||
Revision as of 13:36, 19 October 2010
Homework 6 Solution
Q1.
Matlab code:
Assign the value of parameters and then call the function signalDFT
For example, in case 6 type following command in the command window of Matlab:
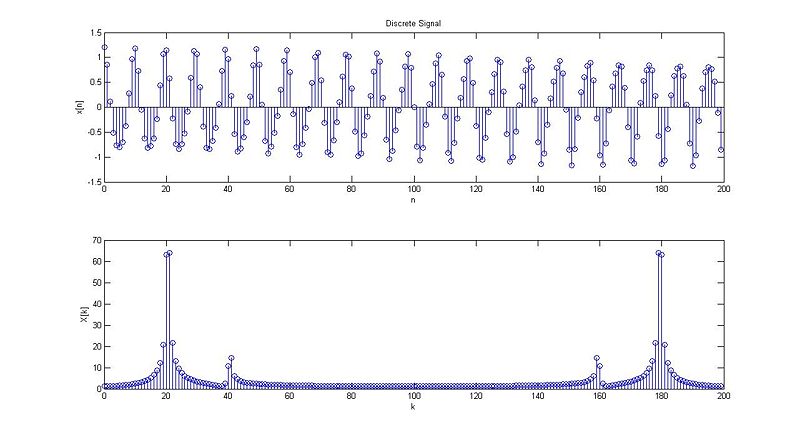
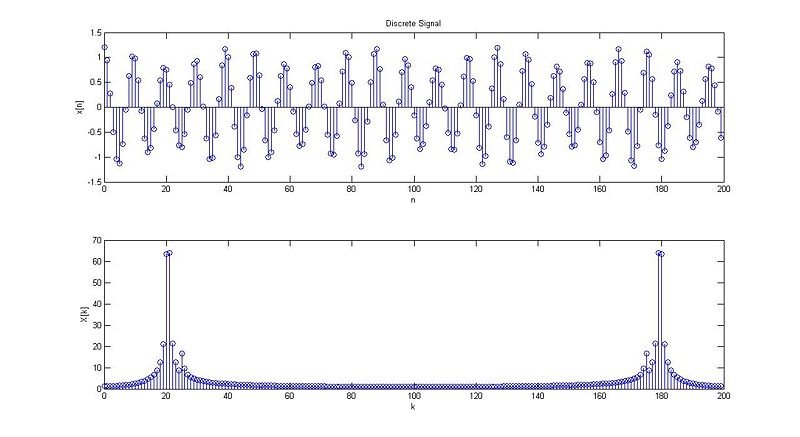
N=20;
w1=0.62831853;
k=0.2;
w2=0.79168135;
[x,X]=signal(w1,w2,k,N);
Plot result:
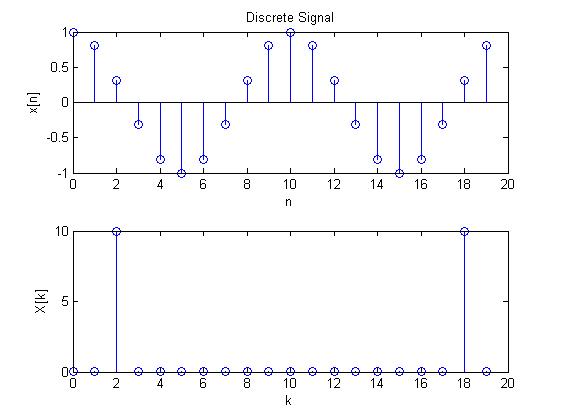
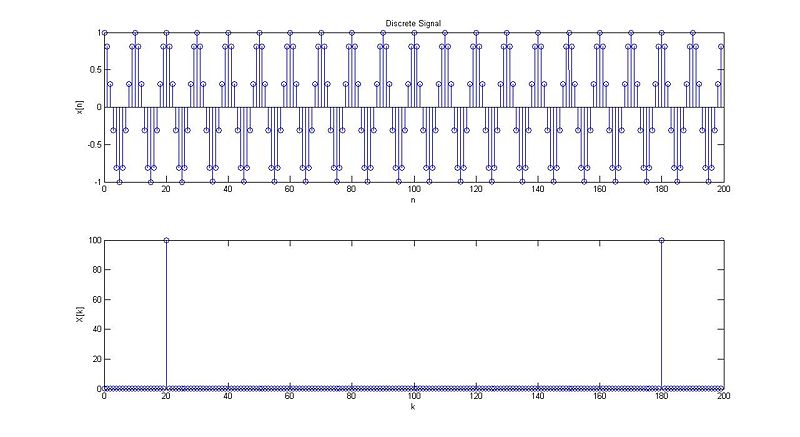
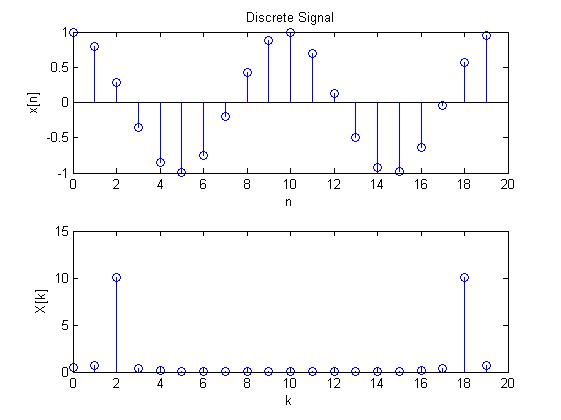
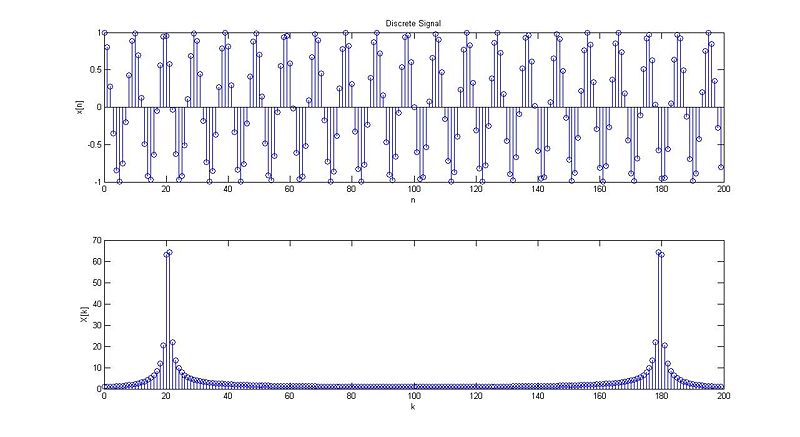
case 1:
case 2:
case 3:
case 4:
case 5:
case 6:
Q2.
Recall the definition of DFT: $ X[k]=\sum_{n=0}^{N-1} x[n]e^{-j2\pi k/N} $
In this question N=8
If we use summation formula to compute DFT, for each k, we need N times complex multiplications and N times complex additions.
In total, we need N*N=64 times of complex multiplications and N*(N-1)=56 times of complex additions.
In decimation-in-time FFT algorithm, we keep on decimating the number of points by 2 until we get 2 points DFT. At most, we can decimate $ v=log_2 N $ times. As a result, we get v levels of DFT. For each level, we need N/2 times of complex multiplications and N times of complex additions.
In total, we need $ \frac{N}{2}log_2 N=12 $N times of complex multiplications and $ Nlog_2 N=24 $ times of complex additions.
Q3.
Denote N is the points number of the input signal's DFT. Then N=6.
1) The normal DFT algorithm: If we use summation formula to compute DFT, according to the analysis of Q2. We need N*N=36 times of complex multiplications and N*(N-1)=30 times of complex additions.
Flow diagram of FFT:
In this FFT algorithm, the computing of DFT is divided into two levels. First, we compute two 3 points DFT, which are DFT of even and odd points.
According to the analysis of Q2, we need N*N=9 times of complex multiplications and N*(N-1)=6 times of complex additions. Since we have to do this twice, we need 9*2=18 times of complex multiplications and 6*2=12 times of complex additions.
Second, we compute the final DFT by combing the first level result. According to the analysis of Q2, we need N/2=3 times of complex multiplications and N=6 times of complex additions.
In total, we need 18+3=21 times of complex multiplications and 12+6=18 times of complex additions.
2)
In this FFT algorithm, the computing of DFT is still divided into two levels. However, we will first compute three 2 points DFT, which are DFT of the first half points and the second half points. According to analysis of Q2, we need N/2=3 times of complex multiplications and N=6 times of complex additions.
Second, we compute the two 3 points DFT using first level result. According to the analysis of Q2, for each 3 points DFT we need N*N=9 times of complex multiplications and N*(N-1)=6 times of complex additions. Since we have to do this twice, we need 9*2=18 times of complex multiplications and 6*2=12 times of complex additions.
In total, we need 3+18=21 times of complex multiplications and 6+12=18 times of complex additions.
Compare 1) and 2), both methods have the same amount of complex operations.
Q4.
Q5.
Q6.
Q7.