(New page: =Discrete-time Fourier transform of a window function= Used in ECE438. ---- Consider the perfect discrete-time window function <math>w[n]= \left\{ \begin{array}{ll} 1,&\text{ if }0 \...) |
|||
| Line 1: | Line 1: | ||
=Discrete-time Fourier transform of a window function= | =Discrete-time Fourier transform of a window function= | ||
Used in [[ECE438]]. | Used in [[ECE438]]. | ||
| + | |||
| + | This page can be used to study the frequency-domain behavior of a discrete-time window function, as its length increases. | ||
| + | |||
---- | ---- | ||
Consider the perfect discrete-time window function | Consider the perfect discrete-time window function | ||
| Line 9: | Line 12: | ||
0, & \text{ else}. | 0, & \text{ else}. | ||
\end{array} | \end{array} | ||
| − | \right.</math> | + | \right.,</math> |
| − | The DTFT of | + | for any integer values of n. Note that N represents the length of the window. The DTFT of this window function is |
<math>W(\omega) =\frac{e^{\frac{-j \omega (N-1)}{2}} \sin\left( \frac{\omega N}{2}\right)}{\sin \left( \frac{\omega}{2} \right)}</math>. | <math>W(\omega) =\frac{e^{\frac{-j \omega (N-1)}{2}} \sin\left( \frac{\omega N}{2}\right)}{\sin \left( \frac{\omega}{2} \right)}</math>. | ||
| Line 27: | Line 30: | ||
[[Image:W_of_omega_N_equal_10000.png|500px]] | [[Image:W_of_omega_N_equal_10000.png|500px]] | ||
| − | Observe the close resemblance of this graph to that of the magnitude of the Fourier transform of the | + | Observe the close resemblance of this graph to that of the magnitude of the Fourier transform of the signal <math>x[n]=1</math>, for any n integer (in other words, an "infinite-length" window). |
---- | ---- | ||
[[ECE438|Back to ECE438]] | [[ECE438|Back to ECE438]] | ||
[[2010_Fall_ECE_438_Boutin|Back to ECE438 Fall 2010]] | [[2010_Fall_ECE_438_Boutin|Back to ECE438 Fall 2010]] | ||
Revision as of 08:43, 27 September 2010
Discrete-time Fourier transform of a window function
Used in ECE438.
This page can be used to study the frequency-domain behavior of a discrete-time window function, as its length increases.
Consider the perfect discrete-time window function
$ w[n]= \left\{ \begin{array}{ll} 1,&\text{ if }0 \leq n < N \\ 0, & \text{ else}. \end{array} \right., $
for any integer values of n. Note that N represents the length of the window. The DTFT of this window function is
$ W(\omega) =\frac{e^{\frac{-j \omega (N-1)}{2}} \sin\left( \frac{\omega N}{2}\right)}{\sin \left( \frac{\omega}{2} \right)} $.
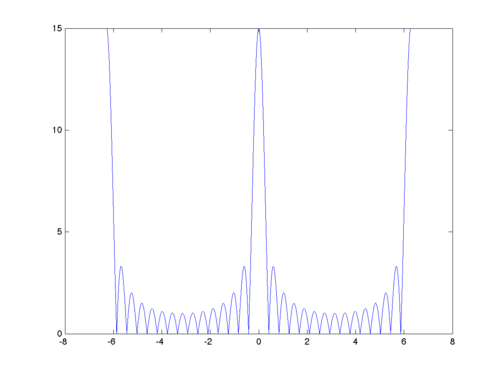
Below is the graph of the magniture of $ W(\omega) $ for $ N=15 $.
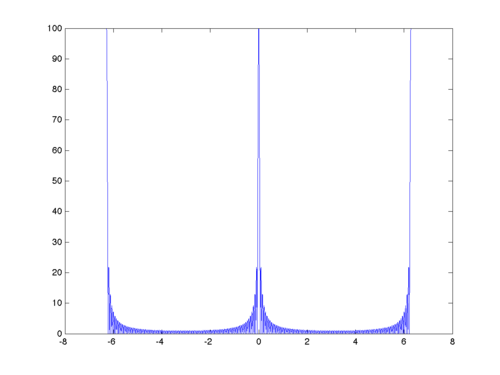
Below is the graph of the magniture of $ W(\omega) $ for $ N=100 $. Observe that the ripples are "thinner" and more numerous than in the previous case of $ N=10 $.
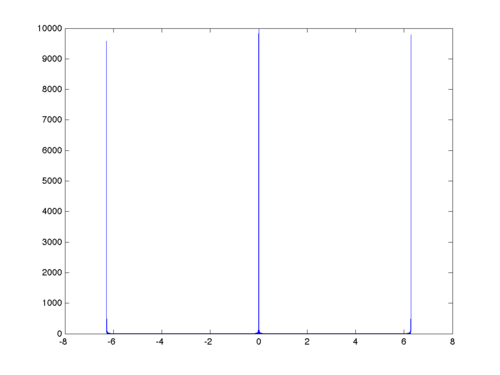
Below is the graph of the magniture of $ W(\omega) $ for $ N=10000 $.
Observe the close resemblance of this graph to that of the magnitude of the Fourier transform of the signal $ x[n]=1 $, for any n integer (in other words, an "infinite-length" window).