| Line 50: | Line 50: | ||
* For the case of our question (<math>L=2</math>), the cut-off frequency is <math>\frac{\pi}{2}</math>. | * For the case of our question (<math>L=2</math>), the cut-off frequency is <math>\frac{\pi}{2}</math>. | ||
| − | * Since <math>x[n]</math> was sampled at 2000 Hz, the output <math>y[n]</math> is the discrete-time signal sampled at the rate of 4000 Hz. | + | * Since <math>x[n]</math> was the discrete-time signal sampled at 2000 Hz, the output <math>y[n]</math> is the discrete-time signal sampled at the rate of 4000 Hz. |
---- | ---- | ||
Latest revision as of 18:52, 20 September 2010
Solution to Q5 of Week 5 Quiz Pool
By Nyquist condition, the sampling frequency must be larger than the twice of maximum signal frequency, in order to avoid the aliasing when sampling.
$ \begin{align} x(t) &= \text{cos}(1000 \pi t) + \text{sin}(1500 \pi t) \\ &= \text{cos}(2\pi \times 500 t) + \text{sin}(2\pi \times 750 t) \end{align} \,\! $
Thus, it consists of two sinusoidal with frequencies equal to 500 Hz and 750 Hz, respectively.
Since the maximum frequency is 750 Hz, the sampling frequency must be greater than 1500 Hz, which is
$ F_s > 2\times 750 = 1500 \text{ Hz} \,\! $
Solution to Q6 of Week 5 Quiz Pool
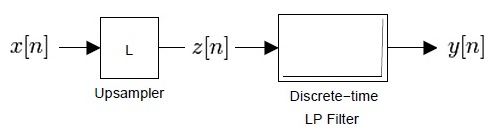
The above figure is the general upsampling process by a factor of $ L $, as you did in Lab 4.
The first upsampler inserts $ L-1 $ zeros in between each sample.
The frequency domain relationship betweeen a signal $ x[n] $ and its upsampled version $ z[n] $ can be shown to be the following,
$ Z(e^{jw}) = X(e^{jwL}) \,\! $
Therefore, the DTFT of $ z[n] $ is simply $ X(e^{jw}) $ compressed in frequency by a factor of $ L $.
$ \Bigg( \text{But note that } z[n] = \left\{\begin{array}{ll}x[m]&n=mL \\ 0& n\neq mL\end{array} \right. \text{, where } m \text{ is an integer.} \Bigg) $
Since $ X(e^{jw}) $ has a period of $ 2\pi $,
$ Z(e^{jw}) \text{ will have a period of } \frac{2\pi}{L}. \,\! $
All the original information of $ x[n] $ will be contained in the interval $ [-\pi/L,\;\pi/L] $ of $ Z(e^{jw}) $
Thus, the unwanted components in the intervals $ [-\pi,\;-\pi/L] $ and $ [\pi/L,\;\pi] $ needs to be filtered out.
Therefore, the cut-off frequency, $ f_c $ of the discrete-time low-pass filter (LPF) is $ f_c=\frac{\pi}{L} $, in general.
And the output $ y[n] $ will be the sequence of samples (discrete-time signal) sampled at the rate of $ Lf_s $ from the original continuous-time signal.
(Note that $ x[n] $ was the sequence of samples (discrete-time signal) sampled at the rate of $ f_s $ from the original continuous-time signal.)
- For the case of our question ($ L=2 $), the cut-off frequency is $ \frac{\pi}{2} $.
- Since $ x[n] $ was the discrete-time signal sampled at 2000 Hz, the output $ y[n] $ is the discrete-time signal sampled at the rate of 4000 Hz.
Back to Lab Week 5 Quiz Pool
Back to ECE 438 Fall 2010 Lab Wiki Page
Back to ECE 438 Fall 2010