| Line 1: | Line 1: | ||
| − | Pick a note frequency < | + | *<span style="color:green"> You are welcome to add comments and questions here!</span> -[[User:zhao148|Zhao]] |
| + | |||
| + | Pick a note frequency <span class="texhtml">''f''<sub>0</sub> = 392''H''''z''</span> | ||
{| | {| | ||
|- | |- | ||
| − | | < | + | | <span class="texhtml">''x''(''t'') = ''c''''o''''s''(2π''f''<sub>0</sub>''t'') = ''c''''o''''s''(2π * 392''t'')</span> |
|- | |- | ||
| <math>a.\ Assign\ sampling\ period\ T_1=\frac{1}{1000}</math> | | <math>a.\ Assign\ sampling\ period\ T_1=\frac{1}{1000}</math> | ||
|- | |- | ||
| − | | <math>2f_0<\frac{1}{T_1}, \ No\ aliasing\ occurs.</math> | + | | <math>2f_0<\frac{1}{T_1}, \ No\ aliasing\ occurs.</math> |
| − | + | ||
|} | |} | ||
<div align="left" style="padding-left: 0em;"> | <div align="left" style="padding-left: 0em;"> | ||
| Line 15: | Line 16: | ||
x_1(n) &=x(nT_1)=cos(2\pi *392nT_1)=cos(2\pi *\frac{392}{1000}n) \\ | x_1(n) &=x(nT_1)=cos(2\pi *392nT_1)=cos(2\pi *\frac{392}{1000}n) \\ | ||
&=\frac{1}{2}\left( e^{-j2\pi *\frac{392}{1000}n} + e^{j2\pi *\frac{392}{1000}n} \right) \\ | &=\frac{1}{2}\left( e^{-j2\pi *\frac{392}{1000}n} + e^{j2\pi *\frac{392}{1000}n} \right) \\ | ||
| − | \end{align} | + | \end{align}</math> |
| − | </math> | + | </div> |
| − | </div> | + | |
{| | {| | ||
| − | | <math>0<2\pi *\frac{392}{1000}<\pi</math> | + | |- |
| + | | <math>0<2\pi *\frac{392}{1000}<\pi</math> | ||
|- | |- | ||
| <math>-\pi<-2\pi *\frac{392}{1000}<0</math> | | <math>-\pi<-2\pi *\frac{392}{1000}<0</math> | ||
| Line 28: | Line 29: | ||
\mathcal{X}_1(\omega) &=2\pi *\frac{1}{2} \left[\delta (\omega -2\pi *\frac{392}{1000}) + \delta (\omega + 2\pi *\frac{392}{1000})\right] \\ | \mathcal{X}_1(\omega) &=2\pi *\frac{1}{2} \left[\delta (\omega -2\pi *\frac{392}{1000}) + \delta (\omega + 2\pi *\frac{392}{1000})\right] \\ | ||
&=\pi \left[\delta (\omega -2\pi *\frac{392}{1000}) + \delta (\omega + 2\pi *\frac{392}{1000})\right] \\ | &=\pi \left[\delta (\omega -2\pi *\frac{392}{1000}) + \delta (\omega + 2\pi *\frac{392}{1000})\right] \\ | ||
| − | \end{align} | + | \end{align}</math> |
| − | </math> | + | </div> |
| − | </div> | + | [[Image:Xw1 singleperiod.jpg]] |
| − | [[Image: | + | |
{| | {| | ||
|- | |- | ||
| Line 38: | Line 39: | ||
| <math>\mathcal{X}_1(\omega)=\pi* rep_{2\pi} \left[\delta (\omega -2\pi *\frac{392}{1000}) + \delta (\omega + 2\pi *\frac{392}{1000})\right]</math> | | <math>\mathcal{X}_1(\omega)=\pi* rep_{2\pi} \left[\delta (\omega -2\pi *\frac{392}{1000}) + \delta (\omega + 2\pi *\frac{392}{1000})\right]</math> | ||
|} | |} | ||
| − | [[Image: | + | |
| + | [[Image:Xw1 multiperiod.jpg]] | ||
| + | |||
{| | {| | ||
| − | |In this situation, no aliasing occurs. In the interval of < | + | |- |
| + | | In this situation, no aliasing occurs. In the interval of <span class="texhtml">[ − π,π]</span>, which represents one period, the frequcy spectrum remains the same as Fig a-1. | ||
|} | |} | ||
| + | |||
{| | {| | ||
|- | |- | ||
| <math>b.\ Assign\ sampling\ period\ T_2=\frac{1}{500}</math> | | <math>b.\ Assign\ sampling\ period\ T_2=\frac{1}{500}</math> | ||
|- | |- | ||
| − | | <math>2f_0>\frac{1}{T_2}, \ Aliasing\ occurs.</math> | + | | <math>2f_0>\frac{1}{T_2}, \ Aliasing\ occurs.</math> |
| − | + | ||
|} | |} | ||
<div align="left" style="padding-left: 0em;"> | <div align="left" style="padding-left: 0em;"> | ||
| Line 54: | Line 58: | ||
x_2(n) &=x(nT_2)=cos(2\pi *392nT_2)=cos(2\pi *\frac{392}{500}n) \\ | x_2(n) &=x(nT_2)=cos(2\pi *392nT_2)=cos(2\pi *\frac{392}{500}n) \\ | ||
&=\frac{1}{2}\left( e^{-j2\pi *\frac{392}{500}n} + e^{j2\pi *\frac{392}{500}n} \right) \\ | &=\frac{1}{2}\left( e^{-j2\pi *\frac{392}{500}n} + e^{j2\pi *\frac{392}{500}n} \right) \\ | ||
| − | \end{align} | + | \end{align}</math> |
| − | </math> | + | </div> |
| − | </div> | + | |
{| | {| | ||
| − | | <math>\pi<2\pi *\frac{392}{500}<2\pi</math> | + | |- |
| + | | <math>\pi<2\pi *\frac{392}{500}<2\pi</math> | ||
|- | |- | ||
| <math>-2\pi<-2\pi *\frac{392}{500}<\pi</math> | | <math>-2\pi<-2\pi *\frac{392}{500}<\pi</math> | ||
| Line 66: | Line 70: | ||
| <math>X_2(f)=\frac{1}{2}\left[\delta (f -\frac{392}{500}) + \delta (f + \frac{392}{500})\right]</math> | | <math>X_2(f)=\frac{1}{2}\left[\delta (f -\frac{392}{500}) + \delta (f + \frac{392}{500})\right]</math> | ||
|} | |} | ||
| − | [[Image: | + | |
| + | [[Image:Xw2 singleperiod.jpg]] | ||
| + | |||
{| | {| | ||
| + | |- | ||
| <math>for\ all\ \omega</math> | | <math>for\ all\ \omega</math> | ||
|- | |- | ||
| Line 74: | Line 81: | ||
| <math>X_2(f)=\frac{1}{2}rep_2\left[\delta (f -\frac{392}{500}) + \delta (f + \frac{392}{500})\right]</math> | | <math>X_2(f)=\frac{1}{2}rep_2\left[\delta (f -\frac{392}{500}) + \delta (f + \frac{392}{500})\right]</math> | ||
|} | |} | ||
| − | [[Image: | + | |
| + | [[Image:Xw2 multiperiod.jpg]] | ||
| + | |||
{| | {| | ||
| − | |In this situation, aliasing DO occurs. In the interval of < | + | |- |
| + | | In this situation, aliasing DO occurs. In the interval of <span class="texhtml">[ − π,π]</span>, which represents one period, the frequcy spectrum is different from Fig b-1. | ||
|} | |} | ||
| − | [[Image: | + | |
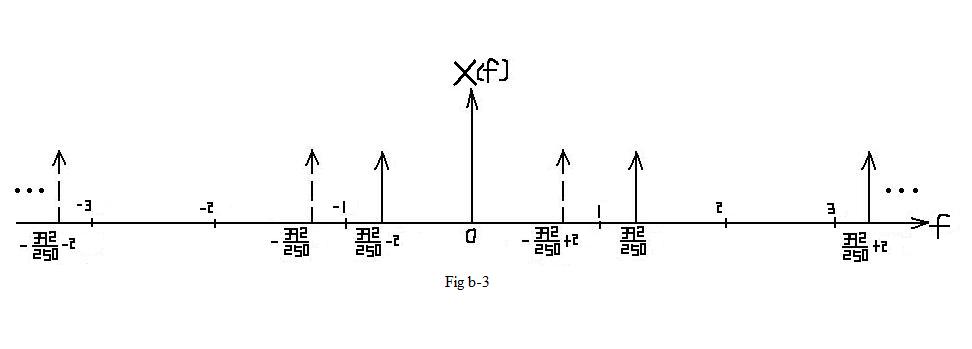
| + | [[Image:Xf2 multiperiod.jpg]] | ||
Revision as of 11:24, 15 September 2010
- You are welcome to add comments and questions here! -Zhao
Pick a note frequency f0 = 392H'z
| x(t) = c'o's(2πf0t) = c'o's(2π * 392t) |
| $ a.\ Assign\ sampling\ period\ T_1=\frac{1}{1000} $ |
| $ 2f_0<\frac{1}{T_1}, \ No\ aliasing\ occurs. $ |
$ \begin{align} x_1(n) &=x(nT_1)=cos(2\pi *392nT_1)=cos(2\pi *\frac{392}{1000}n) \\ &=\frac{1}{2}\left( e^{-j2\pi *\frac{392}{1000}n} + e^{j2\pi *\frac{392}{1000}n} \right) \\ \end{align} $
| $ 0<2\pi *\frac{392}{1000}<\pi $ |
| $ -\pi<-2\pi *\frac{392}{1000}<0 $ |
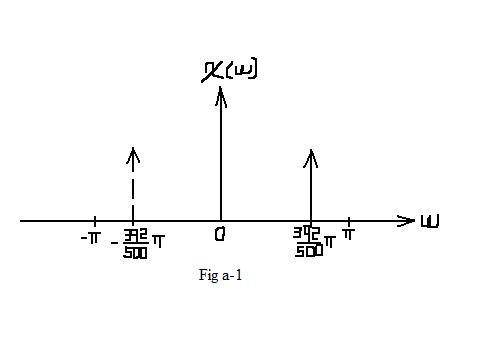
$ \begin{align} \mathcal{X}_1(\omega) &=2\pi *\frac{1}{2} \left[\delta (\omega -2\pi *\frac{392}{1000}) + \delta (\omega + 2\pi *\frac{392}{1000})\right] \\ &=\pi \left[\delta (\omega -2\pi *\frac{392}{1000}) + \delta (\omega + 2\pi *\frac{392}{1000})\right] \\ \end{align} $
| $ for\ all\ \omega $ |
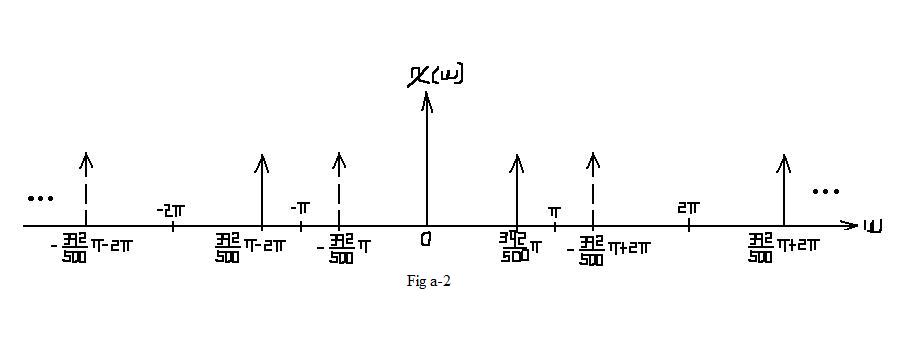
| $ \mathcal{X}_1(\omega)=\pi* rep_{2\pi} \left[\delta (\omega -2\pi *\frac{392}{1000}) + \delta (\omega + 2\pi *\frac{392}{1000})\right] $ |
| In this situation, no aliasing occurs. In the interval of [ − π,π], which represents one period, the frequcy spectrum remains the same as Fig a-1. |
| $ b.\ Assign\ sampling\ period\ T_2=\frac{1}{500} $ |
| $ 2f_0>\frac{1}{T_2}, \ Aliasing\ occurs. $ |
$ \begin{align} x_2(n) &=x(nT_2)=cos(2\pi *392nT_2)=cos(2\pi *\frac{392}{500}n) \\ &=\frac{1}{2}\left( e^{-j2\pi *\frac{392}{500}n} + e^{j2\pi *\frac{392}{500}n} \right) \\ \end{align} $
| $ \pi<2\pi *\frac{392}{500}<2\pi $ |
| $ -2\pi<-2\pi *\frac{392}{500}<\pi $ |
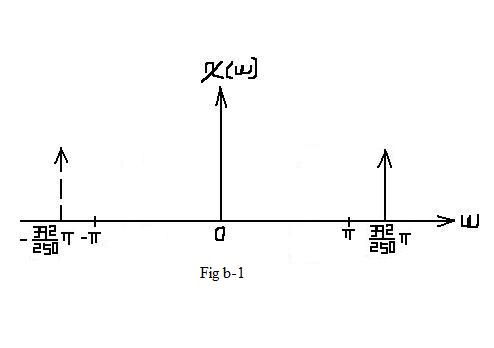
| $ \mathcal{X}_2(\omega)=\pi \left[\delta (\omega -2\pi *\frac{392}{500}) + \delta (\omega + 2\pi *\frac{392}{500})\right] $ |
| $ X_2(f)=\frac{1}{2}\left[\delta (f -\frac{392}{500}) + \delta (f + \frac{392}{500})\right] $ |
| $ for\ all\ \omega $ |
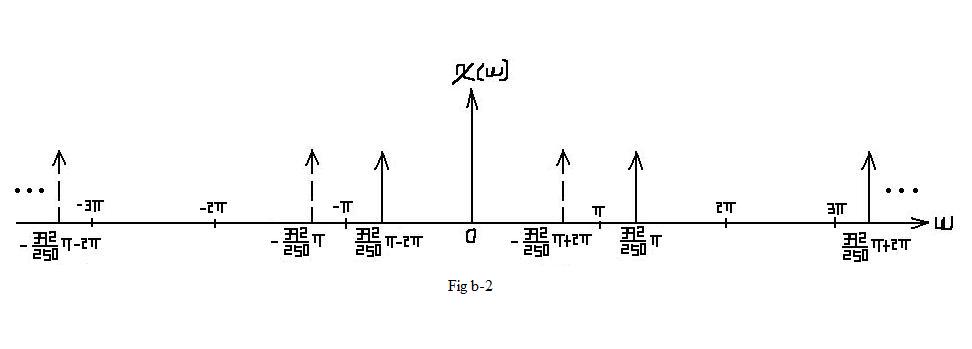
| $ \mathcal{X}_2(\omega)=\pi* rep_{2\pi} \left[\delta (\omega -2\pi *\frac{392}{500}) + \delta (\omega + 2\pi *\frac{392}{500})\right] $ |
| $ X_2(f)=\frac{1}{2}rep_2\left[\delta (f -\frac{392}{500}) + \delta (f + \frac{392}{500})\right] $ |
| In this situation, aliasing DO occurs. In the interval of [ − π,π], which represents one period, the frequcy spectrum is different from Fig b-1. |