Difference between revisions of "Jeffrey's work" - Rhea

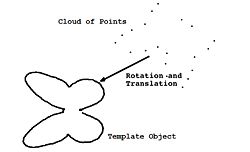
Consider the problem of curve registration, that is, finding the rotation and translation that best maps (i.e., registers) a cloud of points onto a template object, as described on the right.

We first approximate the curve defined by the contour of the template object by an implicit polynomial equation. This yields a bivariate polynomial equation p(x,y) = 0 whose solution set approximates the template contour.

Let (x_i,y_i) , i=1, ..., N be the points of the point cloud. We are looking for the rotation R and the translation T such that p((xi, yi)R + T) = 0 for all i = 1, ..., N. Then we have an overdetermined polynomial equation system with noisy coefficient, which contains N equations and unknown variables R and T. We need to solve this overdetermined polynomial system.