| Line 3: | Line 3: | ||
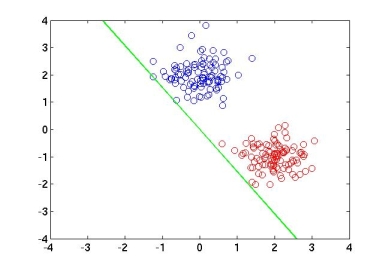
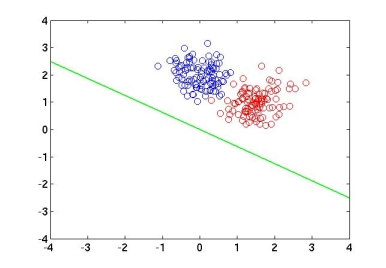
The following plots show the results of my experiment, where the red and the blue circles represent data of two different classes in 2D and the green line represents the direction of the vector '''w''' where the data is projected on. | The following plots show the results of my experiment, where the red and the blue circles represent data of two different classes in 2D and the green line represents the direction of the vector '''w''' where the data is projected on. | ||
| − | [[Image:Fig 1.jpg]] [[Image:Fig 2.jpg]] [[Image:Fig 3.jpg]] | + | [[Image:Fig 1.jpg]] [[Image:Fig 2.jpg]] [[Image:Fig 3.jpg]] |
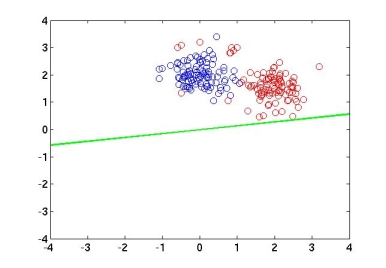
| − | The third plot shows the case where the data is not linearly separable. We can observe that the Fisher | + | The third plot shows the case where the data is not linearly separable. We can observe that the Fisher linear discriminant does not perform that bad in this case and that it always try to find the direction of '''w''' so that there is not much overlap in the projected space. I think that we could use the Fisher linear discriminant in real-world scenarios where there the data is not linearly separable but with small class overlap. However, if the overlap is considerable, we would need to use more complex methods like SVM. |
Revision as of 17:25, 15 April 2010
After learning the Fisher linear discriminant in class and its ability to project data into one dimension so that it can be separated by a threshold, I wanted to evaluate it using non linearly separable data and to observe visually its performance. So I implemented the Fisher discriminant in Matlab and used some synthetic data to visualize how the data is projected onto one dimension.
The following plots show the results of my experiment, where the red and the blue circles represent data of two different classes in 2D and the green line represents the direction of the vector w where the data is projected on.
The third plot shows the case where the data is not linearly separable. We can observe that the Fisher linear discriminant does not perform that bad in this case and that it always try to find the direction of w so that there is not much overlap in the projected space. I think that we could use the Fisher linear discriminant in real-world scenarios where there the data is not linearly separable but with small class overlap. However, if the overlap is considerable, we would need to use more complex methods like SVM.