(New page: == Periodic Function == A function is periodic if there exists a T>0 such that x(t + T) = x(t). Therefore the function sin(x) is periodic because there exists a T = 2pi such that sin(t+ ...) |
|||
| (2 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
| + | =Periodic versus non-periodic functions ([[Homework_1_ECE301Fall2008mboutin|hw1]], [[ECE301]])= | ||
| + | <span style="color:green"> Read the instructor's comments [[hw1periodicECE301f08profcomments|here]]. </span> | ||
| + | |||
== Periodic Function == | == Periodic Function == | ||
| Line 5: | Line 8: | ||
Therefore the function sin(x) is periodic because there exists a T = 2pi such that sin(t+ 2pi) = sin(t). | Therefore the function sin(x) is periodic because there exists a T = 2pi such that sin(t+ 2pi) = sin(t). | ||
| − | + | [[Image:Function sin_ECE301Fall2008mboutin.JPG]] | |
== Non periodic Function == | == Non periodic Function == | ||
A example of a non periodic function is a sloped line, like y = 2x + 1. So when the function is shifted by a time T, y(x+T) it is not the same as the function y(x). | A example of a non periodic function is a sloped line, like y = 2x + 1. So when the function is shifted by a time T, y(x+T) it is not the same as the function y(x). | ||
| + | |||
| + | [[Image:Function_ECE301Fall2008mboutin.JPG]] | ||
Latest revision as of 06:11, 14 April 2010
Periodic versus non-periodic functions (hw1, ECE301)
Read the instructor's comments here.
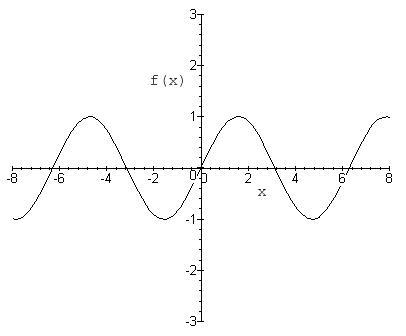
Periodic Function
A function is periodic if there exists a T>0 such that x(t + T) = x(t).
Therefore the function sin(x) is periodic because there exists a T = 2pi such that sin(t+ 2pi) = sin(t).
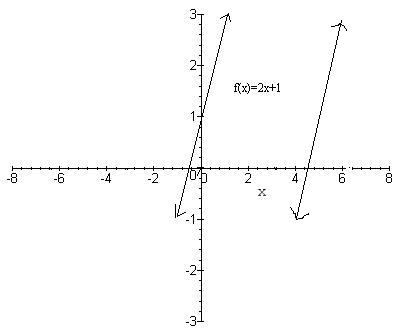
Non periodic Function
A example of a non periodic function is a sloped line, like y = 2x + 1. So when the function is shifted by a time T, y(x+T) it is not the same as the function y(x).