| Line 23: | Line 23: | ||
After 6 hours of coding, and processing the image of my dog "Milo"(shown below), countless times, I am proud to say, that it is | After 6 hours of coding, and processing the image of my dog "Milo"(shown below), countless times, I am proud to say, that it is | ||
"Almost Possible in the Real World" | "Almost Possible in the Real World" | ||
| − | [[Image: | + | [[Image:Milo.jpg]] |
---- | ---- | ||
Revision as of 23:54, 22 September 2009
Discrete Time Interpolation
Mathematically, sure. Realistically? Let's find out.
Introduction
My fascination with the concept of discrete time interpolation began, when I asked Prof. Boutin if a discrete time interpolator, can ideally make a low-resolution image, a high resolution one.
The answer was, yes. Ideally, it can.
The equations that led to the concept seemed impeccable and mathematically, it seemed to make perfect sense.
But essentially, all we are doing is:
- adding zeros in between samples (the result of which looks horrible by the way)
- Low pass filtering,
and Voila! hi-res image. Impossible right?
After 6 hours of coding, and processing the image of my dog "Milo"(shown below), countless times, I am proud to say, that it is
"Almost Possible in the Real World"

Page Map
This page contains
- Application to a simple 1-D signal
- Application to an actual real-world image
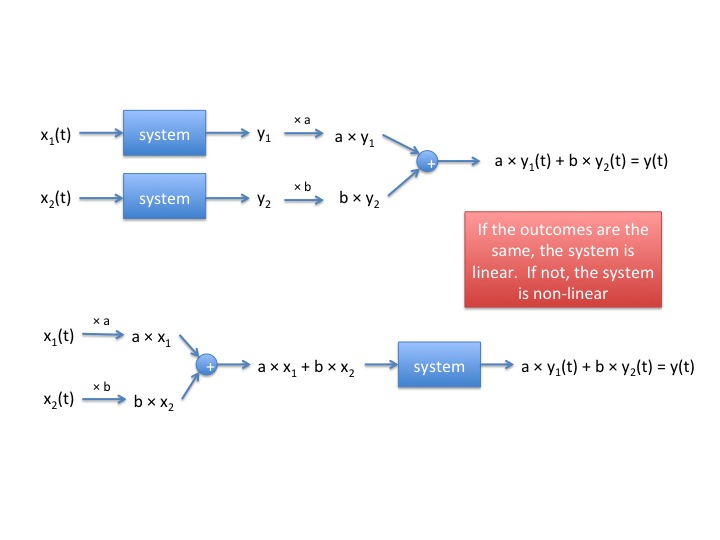
Mathematical Basis
To put the math in a nutshell, so that we can get started with the cool stuff,
let's consider the diagrams below: