| Line 13: | Line 13: | ||
<math> But we had taken the derivative of z(t) to get g(t) (and hence g_k). | <math> But we had taken the derivative of z(t) to get g(t) (and hence g_k). | ||
| − | \therefore z_k = \left ( \frac{g_k}{jk\omega_o} \right ) | + | \therefore z_k = \left ( \frac{g_k}{jk\omega_o} \right ) </math> |
Revision as of 11:26, 1 July 2008
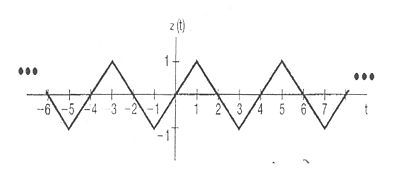
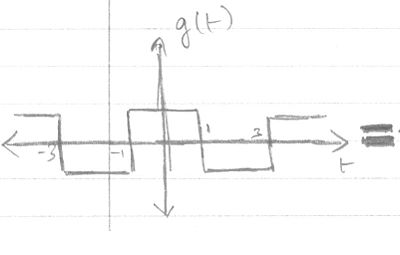
Let $ g(t) = \left ( \frac{dz}{dt} \right ) $
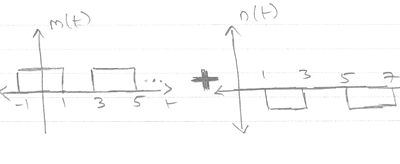
Therefore, $ m_k = \left ( \frac {1}{k\pi} \sin ( \frac {k\pi}{2} ) \right) , n_k = \left( \frac {-1}{k\pi} \sin ( \frac {k\pi}{2} ) e^\frac{-j2k\pi2}{4} \right) $
But $ g_k = m_k + n_k = \left ( \frac {1}{k\pi} \sin ( \frac {k\pi}{2} ) \right) + \left( \frac {-1}{k\pi} \sin ( \frac {k\pi}{2} ) e^\frac{-j2k\pi2}{4} \right) $
$ \therefore g_k = \left ( \frac {1}{k\pi} \sin ( \frac {k\pi}{2} ) \right) + \left( \frac {-1}{k\pi} \sin ( \frac {k\pi}{2} ) (-1)^k \right) $
$ But we had taken the derivative of z(t) to get g(t) (and hence g_k). \therefore z_k = \left ( \frac{g_k}{jk\omega_o} \right ) $