Difference between revisions of "Lecture 25 - Clustering Algorithms OldKiwi" - Rhea

Revision as of 20:44, 20 April 2008

Clustering Methods - A summary

Figure 1

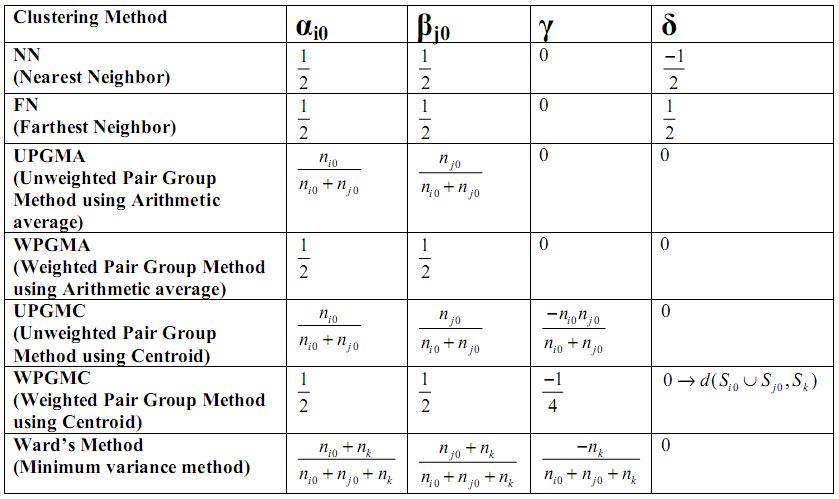
Ward's method is supposedly the best. What this means is when there are natural clusters in the dataset, then almost all of above mentioned methods work well, but of them Ward's method works the best.

But these methods have a serious shortcoming. They tend to find compact clusters because they depend on distances between data points.

• Illustrating figure can be inserted

So, if the natural clustering in data points is elongated and interspersed, these methods may break one elongated cluster into many, and may mix different elongated clusters into one. So, we need feature vectors to find natural clusters, if they are of arbitrary shape and contain arbitrary number of points.

In a high dimension feature space, data points are never adequate. The space is always sparse, and typically distance between any two data points is of the same order. So, the approach used is to project data onto lower dimensions. It doesn't matter which features or combination of features are used to project, because the objective is to have a indexing mechanism for the database.

Figure 3

Algorithms for clustering from feature vector

Called "Partitional clustering" in Jain and Dude as opposed to "hierarchical clustering" Clustering feature vectors = finding separation between clusters but these are not known

Figure 4

<<Picture>>

We have a set of points S Want to find subsets $ S_1 , S_2 , \cdots , S_c $ such that $ S=S_1 \cup S_2 \cup \cdots \cup S_c $ and $ S_i \cap S_j = \phi $

need to define "clustering criteria" i.e., a measure of how natural the clustering is.

if c=2,

consider

$ J=tr(S_m ^{-1} S_w) $

where $ S_w $ is "within class scatter matrix"

$ S_w= \sum _{i=1, X_i \in S_1} ^d ||X_i - \mu _1||^2 + \sum _{i=1, X_i \in S_2} ^d ||X_i - \mu _2||^2 $ (2-1)

$ \mu _1 = \frac{1}{|S_1|} \sum _{X_i \in S_1} X_i $, $ \mu _2 = \frac{1}{|S_2|} \sum _{X_i \in S_2} X_i $ (2-2)

$ S_m $ is "mixture scatter matrix"

$ S_m= \sum _{i=1} ^d ||X_i - \mu||^2 $, $ \mu = \frac{1}{d} \sum _{i=1} ^{d} X_i $ (2-3)

Try to find $ S_1 $ and $ S_2 $ that minimize J.

Exhaustive search procedure

Examnple with 6 pattern $ X_1 , X_2 , \cdots , X_6 $

List all partition of 6 points into 2 sets.

<<Someting>>

Evaluate J for each partition

Cansider other J's

$ J=ln|S_m ^{-1} S_w| $ (2-4)

$ J=tr (S_m) - \mu (tr S_w -c) $ (2-5)

C is fixed constant, $ \mu $ : Largrange multiplier

$ J=\frac{tr(S_m)}{tr(S_w)} $ (2-6)

To speed up search "use iterative procedure"

Pick a partition at random

$ S_1={X_1, X_2, X_3}, S_2= {X_4, X_5, X_6} $ (2-7)

Compute J

Consider effect of moving

$ X_1 $ into $ S_2 \Rightarrow \Delta J_{12} $,

$ X_2 $ into $ S_2 \Rightarrow \Delta J_{22} $,

$ X_3 $ into $ S_3 \Rightarrow \Delta J_{33} $,

$ X_4 $ into $ S_1 \Rightarrow \Delta J_{41} $,

$ X_5 $ into $ S_1 \Rightarrow \Delta J_{51} $,

$ X_6 $ into $ S_1 \Rightarrow \Delta J_{61} $

Apply (Simultaneously) all the moves for which $ \Delta J $ is negative, repeat procedure

OR

Apply the move for which $ \Delta J $ is the most negative repeat procedure

Convergence?

If convergence, global minimum? No idea

If c>2, can use similar procedure

If c is unknown, try c=2,3,4, etc (hierarchical clustering)

Look at evolution of J for c increase (similarity scale)

<<Picture>>

An important J

"Square error criterion"

$ J=\sum _{j=1} ^{c} \sum _{X_i \in S_j}||X_i - \mu _ j||^2 $ (2-8)

where $ \mu _j = \frac{1}{|S_j|} \sum _{X_i \in S_j} X_i $ (2-9)

• Good when clusters are compact, well separated
• Sensitive to outliers

$ J=\sum _{j=1} ^{c} \sum _{X_i \in S_j} ||X_i - \mu_j||_{L1} $ is more robust to outliers

Can use other types of similarity measure

$ S(X_1, X_2)=\frac{X_1 \cdot X_2}{||X_1||||X_2||} $ (2-10)

to speed up optimization of J

Use "Nearest mean reclassification rule"

• choose initial partition $ S_1, S_2 , \cdots , S_c $ (2-11)

• calculate $ \mu _1 , \mu _2 , \cdots , \mu _c $

• reclsssify each $ X_i $ to the class of the nearest mean

• If cluster have changed, repeat

Note: $ X_i $ class of its nearest mean

is same as choosing the move for $ X_i $ that moves $ \Delta J $ as negative as possible because $ J=\sum _{j=1} ^{c} \sum _{X_i \in S_j} ||X_i - \mu _j||^2 $ (2-12)

If $ X_{io} \in S_{jo} \rightarrow X_{io} \in S_{\bar{j0}} $,

$ J \Rightarrow \sum _{j=1} ^{c} \sum _{X_i \in S_j} ||X_i - \mu_j||^2 - ||X_{io}-\mu _{jo}||^2 + ||X_{io} - \mu _{\bar {jo}}||^2 $ (2-13)

$ \Delta J $ is as negative as possible when $ ||X_{io} - \mu _{\bar {jo}}||^2 $ is $ \begin{smallmatrix} min\\ j \end{smallmatrix} ||X_i -\mu _j||^2 $ (2-14)

Can use FORGY, CLUSTER

Observation

$ J= \cdots = \sum _{j=1} ^c \frac{1}{|S_j|} \sum _{X_i \in S_j , X_k \in S_j} \frac{||X_i-X_k||^2}{2} $ (2-15)

This is a distance based clustering method.

No need for feature vector