| Line 6: | Line 6: | ||
The rectangle would have four transformations: | The rectangle would have four transformations: | ||
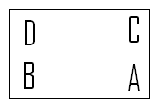
| − | Rotation of 0º (or 360º) : <math>R_{ | + | Rotation of 0º (or 360º) : <math>R_{0}</math> |
[[Image:R0_MA453Fall2008walther.png]] | [[Image:R0_MA453Fall2008walther.png]] | ||
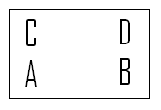
| − | Rotation of 180º: <math>R_{ | + | Rotation of 180º: <math>R_{180}</math> |
[[Image:R180_MA453Fall2008walther.png]] | [[Image:R180_MA453Fall2008walther.png]] | ||
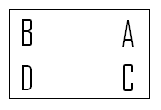
| − | Flip About a Horizontal Axis: H | + | Flip About a Horizontal Axis: <math>H</math> |
[[Image:H_MA453Fall2008walther.png]] | [[Image:H_MA453Fall2008walther.png]] | ||
| − | Flip About a Vertical Axis: V | + | Flip About a Vertical Axis: <math>V</math> |
[[Image:V_MA453Fall2008walther.png]] | [[Image:V_MA453Fall2008walther.png]] | ||
From this, the Cayley table can easily be constructed. | From this, the Cayley table can easily be constructed. | ||
Revision as of 17:32, 7 September 2008
If you name the verticies of the four rectangles A, B, C, and D.
The rectangle would appear thus:
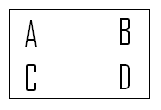
The rectangle would have four transformations:
Rotation of 0º (or 360º) : $ R_{0} $
Rotation of 180º: $ R_{180} $
Flip About a Horizontal Axis: $ H $
Flip About a Vertical Axis: $ V $
From this, the Cayley table can easily be constructed.