(→Relationship to Laplace) |
(→Relationship to Fourier) |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 23: | Line 23: | ||
Likewise the unilateral Z-transform is simply the one-sided Laplace transform of the ideal sampled function. Both assume that the sampled function is zero for all negative time indices. | Likewise the unilateral Z-transform is simply the one-sided Laplace transform of the ideal sampled function. Both assume that the sampled function is zero for all negative time indices. | ||
| − | The | + | The Bilinear transform is a useful approximation for converting continuous time filters (represented in Laplace space) into discrete time filters (represented in z space), and vice versa. To do this, you can use the following substitutions in <math> H(s) </math> or <math> H(z) </math> : |
<math> s =\frac{2}{T} \frac{z-1}{z+1} </math> from Laplace to z (Tustin transformation); | <math> s =\frac{2}{T} \frac{z-1}{z+1} </math> from Laplace to z (Tustin transformation); | ||
<math> z =\frac{2+sT}{2-sT} </math> from z to Laplace. | <math> z =\frac{2+sT}{2-sT} </math> from z to Laplace. | ||
| + | |||
| + | |||
| + | ==Relationship to Fourier== | ||
| + | The Z-transform is a generalization of the discrete-time Fourier transform (DTFT). The DTFT can be found by evaluating the Z-transform <math>X(z)\ </math> at <math>z=e^{j\omega}\ </math> or, in other words, evaluated on the unit circle. In order to determine the frequency response of the system the Z-transform must be evaluated on the unit circle, meaning that the system's region of convergence must contain the unit circle. Otherwise, the DTFT of the system does not exist. | ||
Latest revision as of 16:27, 3 December 2008
Contents
Basic definition of the Z-Transform
The Z-transform of a sequence is defined as $ H(z) = \sum^{\infty}_{n = -\infty} h[n]z^{-n} $
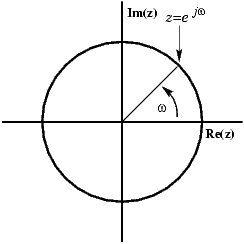
The complex plane
In order to get further insight into the relationship between the Fourier Transform and the Z-Transform it is useful to look at the complex plane or z-plane. Take a look at the complex plane:
The Z-plane is a complex plane with an imaginary and real axis referring to the complex-valued variable z. The position on the complex plane is given by rⅇⅈω , and the angle from the positive, real axis around the plane is denoted by ω. X(z) is defined everywhere on this plane. X(ⅇⅈω) on the other hand is defined only where |z|=1, which is referred to as the unit circle. So for example, ω=1 at z=1 and ω=<apply>π</apply> at z=-1. This is useful because, by representing the Fourier transform as the z-transform on the unit circle, the periodicity of Fourier transform is easily seen.
Region of Convergence
The region of convergence, known as the ROC, is important to understand because it defines the region where the z-transform exists. The ROC for a given x[n] , is defined as the range of z for which the z-transform converges. Since the z-transform is a power series, it converges when x[n]z−n is absolutely summable. Stated differently, $ ROC = \left\{ z : \left|\sum_{n=-\infty}^{\infty}x[n]z^{-n}\right| < \infty \right\} $ must be satisfied for convergence. This is best illustrated by looking at the different ROC's of the z-transforms of αnu[n] and αnu[n−1].
Relationship to Laplace
The bilateral Z-transform is simply the two-sided Laplace transform of the ideally sampled time function
- $ x_{s}(t) = \sum_{n=-\infty}^{\infty} x(nT) \delta(t-nT) = \sum_{n=-\infty}^{\infty} x[n] \delta(t-nT) \ $
where $ x(t) $ is the continuous-time function being sampled, $ x[n]=x(nT) $ the nth sample, $ T $ is the sampling period, and with the substitution: $ z = e^{sT} $.
Likewise the unilateral Z-transform is simply the one-sided Laplace transform of the ideal sampled function. Both assume that the sampled function is zero for all negative time indices.
The Bilinear transform is a useful approximation for converting continuous time filters (represented in Laplace space) into discrete time filters (represented in z space), and vice versa. To do this, you can use the following substitutions in $ H(s) $ or $ H(z) $ :
$ s =\frac{2}{T} \frac{z-1}{z+1} $ from Laplace to z (Tustin transformation);
$ z =\frac{2+sT}{2-sT} $ from z to Laplace.
Relationship to Fourier
The Z-transform is a generalization of the discrete-time Fourier transform (DTFT). The DTFT can be found by evaluating the Z-transform $ X(z)\ $ at $ z=e^{j\omega}\ $ or, in other words, evaluated on the unit circle. In order to determine the frequency response of the system the Z-transform must be evaluated on the unit circle, meaning that the system's region of convergence must contain the unit circle. Otherwise, the DTFT of the system does not exist.