(→AM Demodulation) |
(→AM Demodulation) |
||
| Line 1: | Line 1: | ||
== AM Demodulation == | == AM Demodulation == | ||
| + | |||
| + | [[Image:Hw9_ECE301Fall2008mboutin.JPG]] | ||
<math>r(n)= x(n)cos^2(n \theta)= \frac{1}{2} x(n) + \frac{1}{2}x(n)cos(2n\theta)</math><br> | <math>r(n)= x(n)cos^2(n \theta)= \frac{1}{2} x(n) + \frac{1}{2}x(n)cos(2n\theta)</math><br> | ||
| Line 7: | Line 9: | ||
<math> = X(e^{j\theta}) </math> | <math> = X(e^{j\theta}) </math> | ||
| − | [[Image: | + | [[Image:hw91_ECE301Fall2008mboutin.jpg]] |
Revision as of 16:38, 17 November 2008
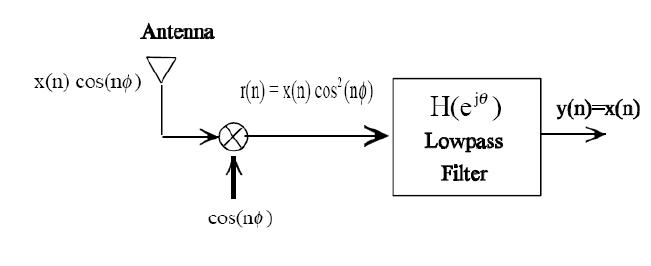
AM Demodulation
$ r(n)= x(n)cos^2(n \theta)= \frac{1}{2} x(n) + \frac{1}{2}x(n)cos(2n\theta) $
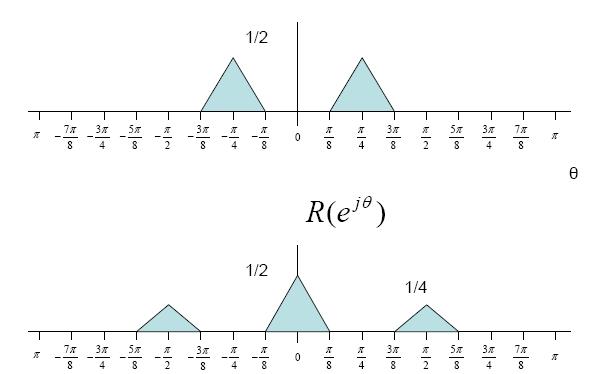
$ Y(e^{j\theta})= R(e^{j\theta})H(e^{j\theta}) $
$ = \frac{1}{2}X(e^{j\theta})+\frac{1}{4}X(e^{j\theta-2\phi})+\frac{1}{4}X(e^{j\theta+2\phi})H(e^{j\theta}) $
$ = X(e^{j\theta}) $