(New page: ==Part 1== Periodic signal Periodic signal turned Non-Periodic ==Part 2== Non-Periodic Signal Non-Periodic Signal turned Periodic) |
(→Part 2) |
||
| (13 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
==Part 1== | ==Part 1== | ||
Periodic signal | Periodic signal | ||
| − | Periodic signal turned Non-Periodic | + | Sampling the signal at a frequency that is a rational multiple of the frequency of the signal will result in a periodic Discrete Time signal. Sampling the signal at a frequency that is not a rational multiple of the frequency of the signal will result in a non-periodic Discrete Time signal. |
| + | |||
| + | My all time favorite CT periodic signal- Sin(t) | ||
| + | <pre> | ||
| + | t = 0:0.02:10; | ||
| + | x = sin(t); | ||
| + | plot(t,x) | ||
| + | grid on | ||
| + | </pre> | ||
| + | [[image: SIN.jpg]] | ||
| + | |||
| + | Periodic signal turned Non-Periodic, DT non-periodic signal | ||
| + | <pre> | ||
| + | t = 0:0.5:10; | ||
| + | x = sin((1/(2*pi))*t); | ||
| + | plot(t,x) | ||
| + | grid on | ||
| + | stem(t,x) | ||
| + | </pre> | ||
| + | [[image: SINdt.jpg]] | ||
| + | |||
==Part 2== | ==Part 2== | ||
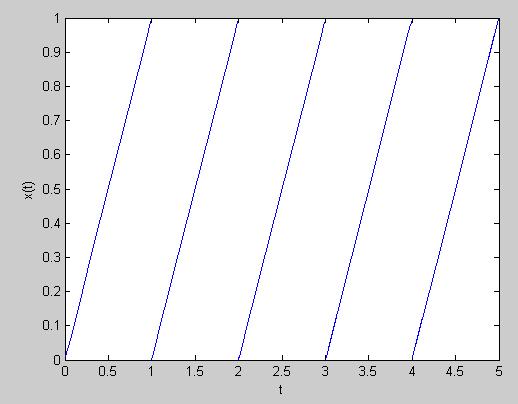
| − | Non-Periodic Signal | + | Non-Periodic Signal and Non-Periodic Signal turned Periodic |
| − | Non-Periodic Signal turned Periodic | + | |
| + | Using x(t) = t | ||
| + | |||
| + | [[Image:Rampsjp_ECE301Fall2008mboutin.JPG]] | ||
| + | |||
| + | Using image from Jacob Pfister. | ||
Latest revision as of 16:10, 12 September 2008
Part 1
Periodic signal Sampling the signal at a frequency that is a rational multiple of the frequency of the signal will result in a periodic Discrete Time signal. Sampling the signal at a frequency that is not a rational multiple of the frequency of the signal will result in a non-periodic Discrete Time signal.
My all time favorite CT periodic signal- Sin(t)
t = 0:0.02:10; x = sin(t); plot(t,x) grid on
Periodic signal turned Non-Periodic, DT non-periodic signal
t = 0:0.5:10; x = sin((1/(2*pi))*t); plot(t,x) grid on stem(t,x)
Part 2
Non-Periodic Signal and Non-Periodic Signal turned Periodic
Using x(t) = t
Using image from Jacob Pfister.