| Line 7: | Line 7: | ||
First I sample the signal y(t)=cos(t) at 100 Hz and so we get the following discrete signal which is periodic | First I sample the signal y(t)=cos(t) at 100 Hz and so we get the following discrete signal which is periodic | ||
| + | the matlab code is as follows | ||
| + | <pre> | ||
| + | t=[0:0.01:10] | ||
| + | y=cos(2*pi*t); | ||
| + | stem(t,y); xlabel('sec'); | ||
| + | </pre> | ||
[[Image:periodic_goklani_ECE301Fall2008mboutin.jpg]] | [[Image:periodic_goklani_ECE301Fall2008mboutin.jpg]] | ||
| Line 18: | Line 24: | ||
* Now if I sample the signal y(t)=cos(t) at 22.22 Hz then we get the following discrete signal which is not periodic | * Now if I sample the signal y(t)=cos(t) at 22.22 Hz then we get the following discrete signal which is not periodic | ||
| + | the matlab code is as follows | ||
| + | <pre> | ||
| + | t=[0:0.045:10] | ||
| + | y=cos(2*pi*t); | ||
| + | stem(t,y); xlabel('sec'); | ||
| + | </pre> | ||
Latest revision as of 20:44, 11 September 2008
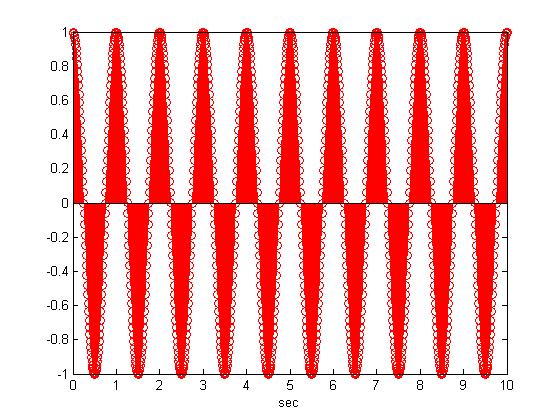
I choose y(t)=cos(t) as my continous signal. There is no doubt that y(t)=cos(t) is periodic because cos(t + T) = cos(t) where its fundamental period is 2*π
Periodic Function
First I sample the signal y(t)=cos(t) at 100 Hz and so we get the following discrete signal which is periodic the matlab code is as follows
t=[0:0.01:10]
y=cos(2*pi*t);
stem(t,y); xlabel('sec');
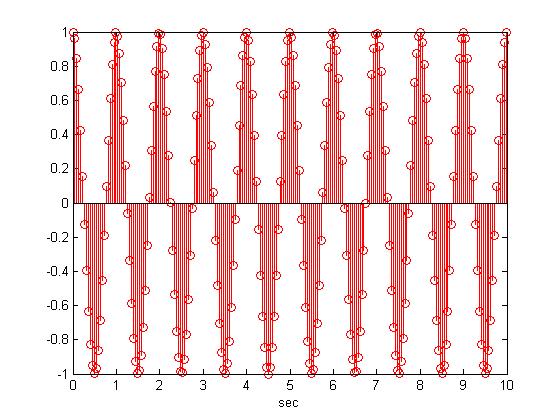
Non periodic funtion
- Now if I sample the signal y(t)=cos(t) at 22.22 Hz then we get the following discrete signal which is not periodic
the matlab code is as follows
t=[0:0.045:10]
y=cos(2*pi*t);
stem(t,y); xlabel('sec');
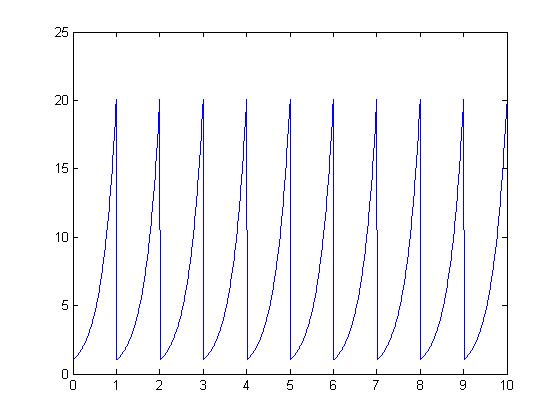
Recurring non periodic function = periodic
Now let us shift the non periodic function y(t)= $ {e^{3t}} $
we use the following matlab code
%referred the code of paul sceffler
clc
clear
t=0.01:.01:1;
x=exp(3*t);
i=[];
for d=1:10
i=[i,x];
end
t=[0.01:.01:10];
plot(t,i)
we see above that the non-periodic signal is now periodic