(→Periodic Signals Revisited) |
(→) |
||
| (10 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | [[Homework 2_ECE301Fall2008mboutin]] - [[HW2-A Phil Cannon_ECE301Fall2008mboutin|'''A''']] - [[HW2-B Phil Cannon_ECE301Fall2008mboutin|'''B''']] - [[HW2-C Phil Cannon_ECE301Fall2008mboutin|'''C''']] - [[HW2-D Phil Cannon_ECE301Fall2008mboutin|'''D''']] - [[HW2-E Phil Cannon_ECE301Fall2008mboutin|'''E''']] | ||
== Periodic Signals Revisited == | == Periodic Signals Revisited == | ||
| − | 1. By sampling at different frequencies the | + | 1. By sampling at different frequencies the signal <math>y=sin(x)\!</math> can appear as both periodic and non-periodic in DT. For example: |
<math>y(x)=sin(x) \!</math> in CT | <math>y(x)=sin(x) \!</math> in CT | ||
| Line 8: | Line 9: | ||
<math>y[n]=sin[n] \!</math> with a sample rate of 1 | <math>y[n]=sin[n] \!</math> with a sample rate of 1 | ||
[[Image:Samprate1_ECE301Fall2008mboutin.jpg]] | [[Image:Samprate1_ECE301Fall2008mboutin.jpg]] | ||
| + | |||
| + | <math>y[n]=sin[n] \!</math> with a sample rate of <math>pi/4 \!</math> | ||
| + | [[Image:Samprate2_ECE301Fall2008mboutin.jpg]] | ||
| + | |||
| + | <br> | ||
| + | The second graph has no integer value of N where y[n]=y[n+N], thus it is non-periodic. | ||
| + | The third graph clearly shows there is an integer value of N where y[n]=y[n+N], thus it is periodic. | ||
| + | |||
| + | <br> | ||
| + | <br> | ||
| + | == == | ||
| + | 2. By adding up several cycles of the function <math>y(x)=x^2\!</math> where <math>x=[0, 10]\!</math> we can turn a non-periodic signal into a periodic signal: | ||
| + | |||
| + | [[Image:Xsquare_ECE301Fall2008mboutin.jpg]] | ||
| + | [[Image:Xsquare2_ECE301Fall2008mboutin.jpg]] | ||
Latest revision as of 09:10, 12 September 2008
Homework 2_ECE301Fall2008mboutin - A - B - C - D - E
Periodic Signals Revisited
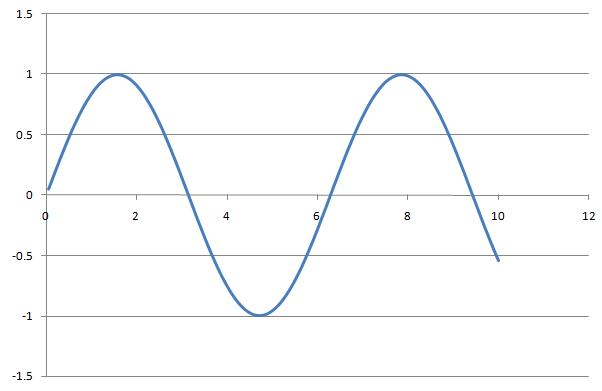
1. By sampling at different frequencies the signal $ y=sin(x)\! $ can appear as both periodic and non-periodic in DT. For example:
$ y[n]=sin[n] \! $ with a sample rate of 1
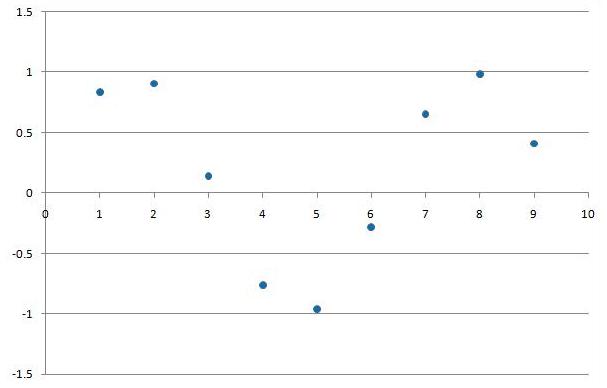
$ y[n]=sin[n] \! $ with a sample rate of $ pi/4 \! $
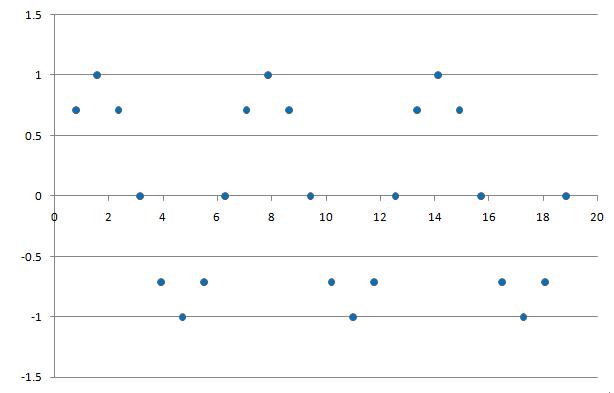
The second graph has no integer value of N where y[n]=y[n+N], thus it is non-periodic.
The third graph clearly shows there is an integer value of N where y[n]=y[n+N], thus it is periodic.
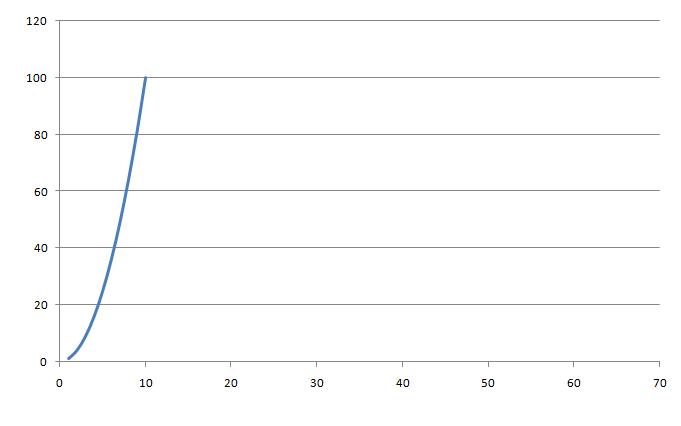
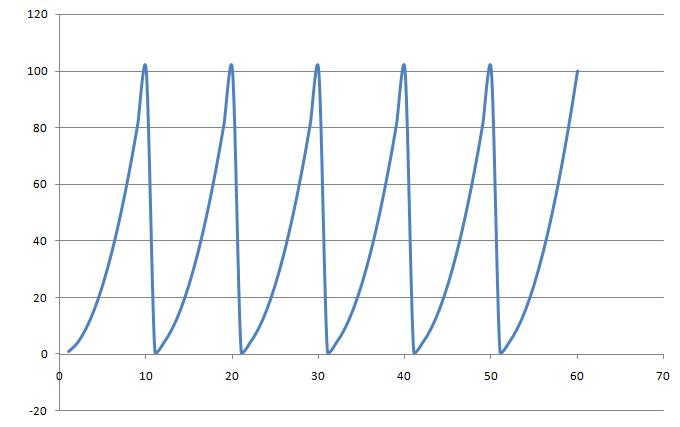
2. By adding up several cycles of the function $ y(x)=x^2\! $ where $ x=[0, 10]\! $ we can turn a non-periodic signal into a periodic signal: