(→Linearity and Time Invariance) |
|||
| Line 1: | Line 1: | ||
| − | |||
== Linearity and Time Invariance == | == Linearity and Time Invariance == | ||
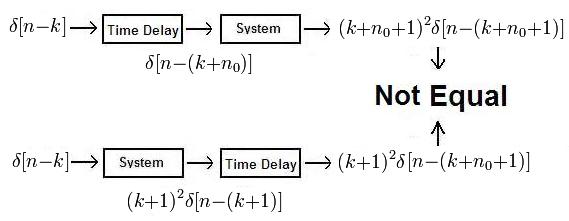
a). This system cannot be time-invarient. This can be proven by using the 3rd definition of Time Invariance given in class: | a). This system cannot be time-invarient. This can be proven by using the 3rd definition of Time Invariance given in class: | ||
[[Image:Hw2E_ECE301Fall2008mboutin.jpg]] | [[Image:Hw2E_ECE301Fall2008mboutin.jpg]] | ||
| + | |||
| + | <br> | ||
| + | <br> | ||
| + | |||
| + | b). Assuming the system were linear it would require an input <math>X[n]=u[n]\!</math> to yield <math>Y[n]=u[n-1]\!</math>. | ||
Revision as of 16:03, 11 September 2008
Linearity and Time Invariance
a). This system cannot be time-invarient. This can be proven by using the 3rd definition of Time Invariance given in class:
b). Assuming the system were linear it would require an input $ X[n]=u[n]\! $ to yield $ Y[n]=u[n-1]\! $.