(→Part 2) |
|||
| (7 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | == Part 1 == | ||
| + | |||
Seems like a lot of people used the cosine function in hw1 so thats the one i'll use now. | Seems like a lot of people used the cosine function in hw1 so thats the one i'll use now. | ||
| + | <pre> | ||
| + | %{ | ||
| + | Jeremiah Wise | ||
| + | 9/11/08 | ||
| + | HW #2 Part A 1 | ||
| + | |||
| + | This program plots and displays a cosine wave | ||
| + | in DT. The first plot is periodic and the second | ||
| + | is not. | ||
| + | %} | ||
| + | |||
| + | |||
| + | %Periodic signal | ||
| + | |||
| + | delta = pi/100; | ||
| + | n = [0 : delta : 6 * pi]; | ||
| + | |||
| + | plot(n, cos(n), '.'); | ||
| + | title('Periodic cosine function'); | ||
| + | xlabel('n'); | ||
| + | ylabel('cos(n)'); | ||
| + | |||
| + | %Non-Periodic Signal | ||
| + | figure(2) | ||
| + | |||
| + | delta = 1; | ||
| + | n = [0 : delta : 6 * pi]; | ||
| + | |||
| + | plot(n, cos(n), '.'); | ||
| + | title('Non-Periodic cosine function'); | ||
| + | xlabel('n'); | ||
| + | ylabel('cos(n)'); | ||
| + | |||
| + | </pre> | ||
[[Image:PeriodicSignal_ECE301Fall2008mboutin.jpg]] | [[Image:PeriodicSignal_ECE301Fall2008mboutin.jpg]] | ||
[[Image:Non-PeriodicSignal_ECE301Fall2008mboutin.jpg]] | [[Image:Non-PeriodicSignal_ECE301Fall2008mboutin.jpg]] | ||
| + | |||
| + | |||
| + | == Part 2 == | ||
| + | |||
| + | If we use the function <math>x[n]=e^{-n/10}*sin(2n)</math> and add shifted copies of the signal together, we obtain a periodic signal. | ||
| + | |||
| + | Note: The exponent in the above equation was changed from -n/20 (from hw1) to -n/10 because it made the graph look better. | ||
| + | |||
| + | <pre> | ||
| + | %{ | ||
| + | Jeremiah Wise | ||
| + | 9/12/08 | ||
| + | HW #2 Part A 2 | ||
| + | |||
| + | This program plots and displays a function that has been made periodic | ||
| + | by adding together shifted copies of that function. | ||
| + | %} | ||
| + | |||
| + | delta = 1 / 1000; | ||
| + | n = [0 : delta : 10 * pi]; | ||
| + | |||
| + | x = exp(-n / 10) .* sin(2 * n); | ||
| + | |||
| + | for k = 1 : 1 : 2 | ||
| + | n = [n (n + k*10*pi)]; | ||
| + | x = [x x]; | ||
| + | end | ||
| + | |||
| + | plot(n,x); | ||
| + | title('Shifted Copies of a Non-Periodic Signal'); | ||
| + | xlabel('n'); | ||
| + | ylabel('x[n]'); | ||
| + | </pre> | ||
| + | |||
| + | [[Image:partA2_ECE301Fall2008mboutin.jpg]] | ||
Latest revision as of 08:59, 12 September 2008
Part 1
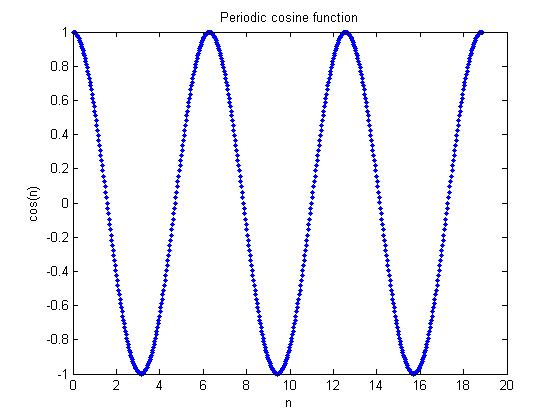
Seems like a lot of people used the cosine function in hw1 so thats the one i'll use now.
%{
Jeremiah Wise
9/11/08
HW #2 Part A 1
This program plots and displays a cosine wave
in DT. The first plot is periodic and the second
is not.
%}
%Periodic signal
delta = pi/100;
n = [0 : delta : 6 * pi];
plot(n, cos(n), '.');
title('Periodic cosine function');
xlabel('n');
ylabel('cos(n)');
%Non-Periodic Signal
figure(2)
delta = 1;
n = [0 : delta : 6 * pi];
plot(n, cos(n), '.');
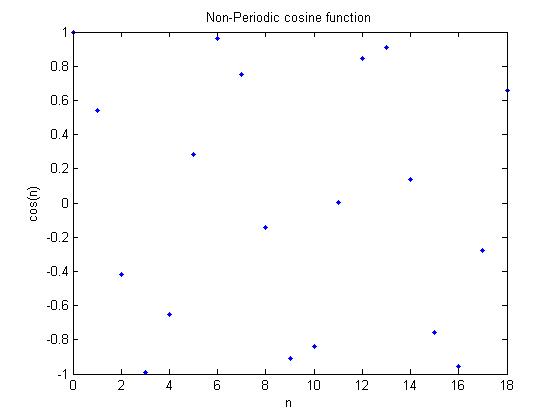
title('Non-Periodic cosine function');
xlabel('n');
ylabel('cos(n)');
Part 2
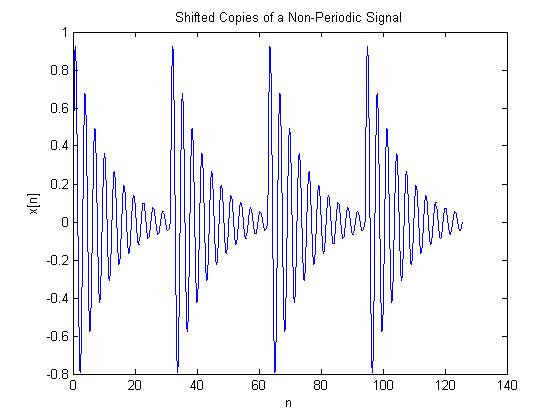
If we use the function $ x[n]=e^{-n/10}*sin(2n) $ and add shifted copies of the signal together, we obtain a periodic signal.
Note: The exponent in the above equation was changed from -n/20 (from hw1) to -n/10 because it made the graph look better.
%{
Jeremiah Wise
9/12/08
HW #2 Part A 2
This program plots and displays a function that has been made periodic
by adding together shifted copies of that function.
%}
delta = 1 / 1000;
n = [0 : delta : 10 * pi];
x = exp(-n / 10) .* sin(2 * n);
for k = 1 : 1 : 2
n = [n (n + k*10*pi)];
x = [x x];
end
plot(n,x);
title('Shifted Copies of a Non-Periodic Signal');
xlabel('n');
ylabel('x[n]');