(→Linear Systems) |
(→Example of a Linear System) |
||
| Line 12: | Line 12: | ||
Let <math>y(t)=x(t) \!</math>. Then: | Let <math>y(t)=x(t) \!</math>. Then: | ||
| − | <math> | + | [[Image:Linsystempjcannon_ECE301Fall2008mboutin.JPG]] |
| + | |||
| + | Thus, the system <math>y(t)=x(t)\!</math> is linear. | ||
Revision as of 11:39, 11 September 2008
Linear Systems
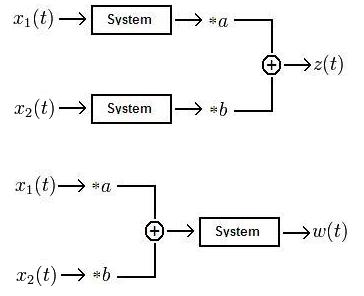
Because we are engineers we will use a picture to describe a linear system:
Where $ a \! $ and $ b\! $ are real or complex. The system is defined as linear if $ z(t)=w(t)\! $
In other words, if in one scenario we have two signals put into a system, multiplied by a variable, then summed together, the output should equal the output of a second scenario where the signals are multiplied by a variable, summed together, then put through the same system. If this is true, then the system is defined as linear.
Example of a Linear System
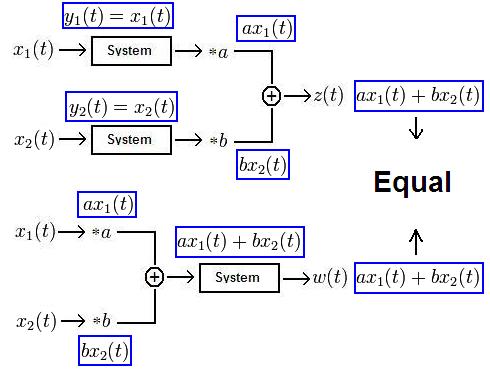
Let $ y(t)=x(t) \! $. Then:
Thus, the system $ y(t)=x(t)\! $ is linear.