| (5 intermediate revisions by the same user not shown) | |||
| Line 18: | Line 18: | ||
This graph is non-periodic at this sampling due to the fact that the function cannot find good values to evaluate the system for integer values that are not multiples of pi. | This graph is non-periodic at this sampling due to the fact that the function cannot find good values to evaluate the system for integer values that are not multiples of pi. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | == Part 2 == | ||
| + | |||
| + | I also referenced Nicholas Browdues non periodic function from homework 1. His function was: | ||
| + | |||
| + | x(t) = e( − t / 20) * sin(2t) | ||
| + | |||
| + | <pre> | ||
| + | t=0:0.1:8*pi | ||
| + | x = exp(-t / 20) .* sin(2*t) | ||
| + | plot(t,x,'--o') | ||
| + | </pre> | ||
| + | |||
| + | <pre> | ||
| + | t=0:0.1:8*pi | ||
| + | x = exp(-t / 20) .* sin(2*t) | ||
| + | plot(t,x, '--o') | ||
| + | hold on | ||
| + | plot(t,x, '--o') | ||
| + | t=8*pi:0.1:24*pi; | ||
| + | hold off | ||
| + | </pre> | ||
| + | |||
| + | |||
| + | [[Image:thing4_ECE301Fall2008mboutin.jpg]] | ||
Latest revision as of 12:17, 12 September 2008
Periodic Function
I chose the function that Nicholas Browdues has used in the previous Homework 1 assignment as my reference signal. x(t)=sin(t) from 0 to 8*pi
This function is periodic as long as it is evaluated at values of 2*pi invtervals.
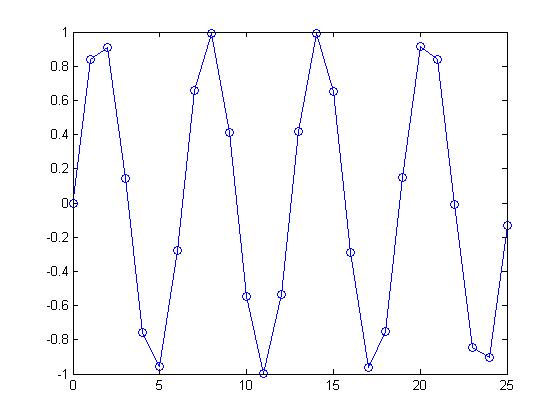
This is the same function but its values have been taken in Discrete time.
t=0:1:25 x=sin(t) plot(t, x, '-o')
This graph is non-periodic at this sampling due to the fact that the function cannot find good values to evaluate the system for integer values that are not multiples of pi.
Part 2
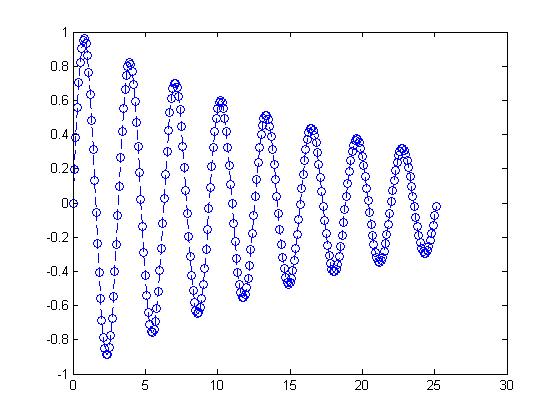
I also referenced Nicholas Browdues non periodic function from homework 1. His function was:
x(t) = e( − t / 20) * sin(2t)
t=0:0.1:8*pi x = exp(-t / 20) .* sin(2*t) plot(t,x,'--o')
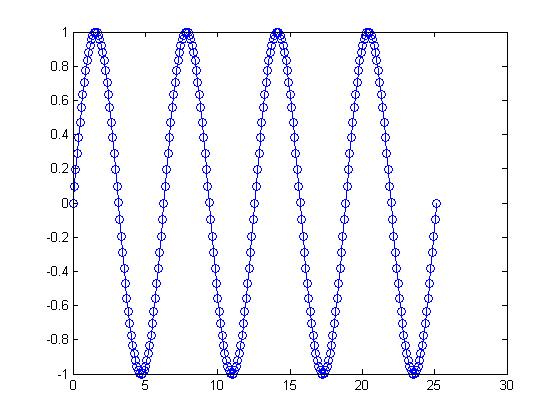
t=0:0.1:8*pi x = exp(-t / 20) .* sin(2*t) plot(t,x, '--o') hold on plot(t,x, '--o') t=8*pi:0.1:24*pi; hold off