(→Part 1) |
(→Part 1) |
||
| Line 7: | Line 7: | ||
'''Periodic Signal in DT:''' | '''Periodic Signal in DT:''' | ||
| − | If sampled at <math>period=0.1</math>, the function | + | If <math>x(t)</math> is sampled at <math>period=0.1</math>, the function |
<math>\,y[n]=x[0.1n]=2cos(\frac{2\pi n}{10})\,</math> | <math>\,y[n]=x[0.1n]=2cos(\frac{2\pi n}{10})\,</math> | ||
| Line 15: | Line 15: | ||
<math>\,y[n]=y[n+10N], \forall N\in Z\,</math> | <math>\,y[n]=y[n+10N], \forall N\in Z\,</math> | ||
| − | + | ||
| + | This can be seen in the following plot (notice how the values lines up horizontally) | ||
| + | |||
| + | [[Image:Jkubasci dt periodic_ECE301Fall2008mboutin.jpg]] | ||
| + | |||
| + | '''Non-Periodic Signal in DT:''' | ||
| + | |||
| + | However, if <math>x(t)</math> is sampled at <math>period=\frac{1}{2\pi}</math>, the function | ||
| + | |||
| + | <math>\,z[n]=x[\frac{n}{2\pi }]=2cos(t)\,</math> | ||
== Part 2 == | == Part 2 == | ||
Revision as of 12:14, 11 September 2008
Part 1
The function was chosen at random from HW1: HW1.4 Hang Zhang - Periodic vs Non-period Functions_ECE301Fall2008mboutin
$ \,x(t)=2cos(2\pi t)\, $
Periodic Signal in DT:
If $ x(t) $ is sampled at $ period=0.1 $, the function
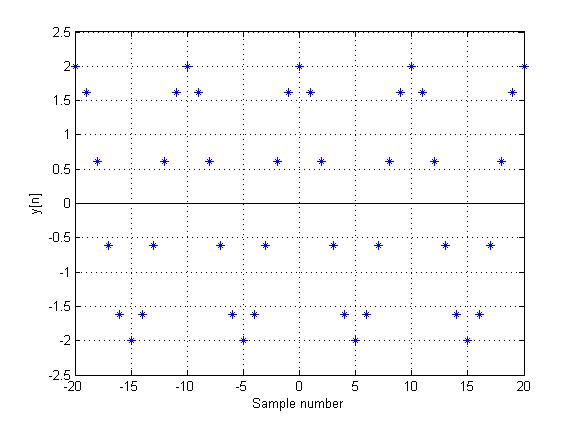
$ \,y[n]=x[0.1n]=2cos(\frac{2\pi n}{10})\, $
would be periodic, since
$ \,y[n]=y[n+10N], \forall N\in Z\, $
This can be seen in the following plot (notice how the values lines up horizontally)
Non-Periodic Signal in DT:
However, if $ x(t) $ is sampled at $ period=\frac{1}{2\pi} $, the function
$ \,z[n]=x[\frac{n}{2\pi }]=2cos(t)\, $