The constitutional right of equal vote vs weighted voting: historical events and the Banzhaf power index
A team project for MA279, Fall 2013
Team members: Shuaijia Dai, Bo Ling, Rustam Orazaliyev, Matthew D Parr, Christopher Patrick
Introduction
Choices we make determine the life we live. However, not everything depends on ourselves. There are situations that affect lives of many people, that is why not all decisions that can be made by only one person, instead a group of involved people must reach a consensus. In such situations people vote to make a decision. The vast majority of developed countries provide their citizens a right to vote. For example, according to Section II, of 28th Amendment to the US Constitution, citizens of the United States have a right to vote and to participate in elections on an equal basis. In addition to the equal voting system, in various situations people also use weighted voting system which does not assume that all people are equal. However, despite the clear usefulness of weighted voting system, it can also create unintentional problems which will be covered further.
Equal vote
An equal voting system refers to a system where every players vote has the same weight in an election. This principle is commonly associated with the phrase "one person, one vote", based on the idea that every person that votes gets a single, equal vote in the election. In an equal voting system, the quota is typically met by a simple majority. But in some cases, a stronger or lesser representation must be met to meet the quota. For example, for the U.S. House of Representatives, votes are counted aloud. But if someone challenges the Speaker of the House on the count and demands a recorded count, where votes are written down, only a one fifth vote is needed for the recount. In this case the quota is note the majority, but rather is one fifth. Referring to the United States and more specifically the idea of weighted voting versus equal voting refers more specifically to the idea that ever American registered voter has an equal say in the Presidential election and that there is no Electoral College or other weighted voting system.
Equal votes are not commonplace in many election scenarios. However one place that equal voting may be implemented most frequently is in some specific town council meetings where laws require certain governmental issues be voted on by the entire town population with equal vote. This classic example of democracy can be pictured by a town showing up to a town hall meeting to vote on simple matters relating to the town. However this is very rare because there simply aren't many towns governed by town councils anymore. That being said, many legislative bodies use equal voting systems when they vote to pass Bills. For example in the Indiana House of Representatives, each of the 100 elected members gets an equal say in whether or not a bill is passed by the Indiana House of Representatives. That being said, it is not truly an equal voting method because for the bill to pass it needs to pass in the Senate as well. But, strictly referring to passing the bill in the House, the method used is equal voting. Outside of legislative bodies and town councils, equal voting is not a supremely popular way to vote. It is often used in schools or other small organizations to elect officials, but large companies, important organizations, and government bodies often use a weighted voting system.
Equal voting in the United States does not have much of a history in the United States presidential election because there has always been the Electoral College since the implementation of the Constitution in 1787. Prior to the Constitution the Articles of Confederation merely brought the states together with no president, so there was no opportunity for such equal voting. However equal voting does have a long history in the United States, as previously stated, in situations such as legislative voting in the U.S. House of Representatives, the Senate, state and local legislative bodies. Equal voting is an important part of American culture and voting, however it does not have a place in United States Presidential election history.
A Look at Weighted Voting
A weighted voting system is one in which the players of such a system hold varying amounts of votes. This differing amount of votes for each player is considered the voting weight of the player. It is completely likely that different players will hold differing weights. We say the voter i has a weight of wi. These weights are important when trying to decide the winner of an election. The quota q is the minimum amounts to win said election, and since the voting system is weighted, only certain combinations of wi will decide a winner. This quota should be at least a majority of the sum of wi to prevent ties, and it is less or equal to the sum of the weights [1].
An example of weighted voting used today comes from the World Bank. The World Bank uses weighted voting with its members and board according to the amount of shares the member holds. Each member receives one vote per share of capital stock he or she holds. Therefore, those with higher share holdings will own a higher weight when voting. In fact, this is the most common use of weighted voting today. People involved with shareholder meetings, such as a businesses board of directors, need a voting system that reflects a player’s involvement in that organization. Those with higher shares and investments in a company tend to want to have more weight assigned to their votes in board meetings. Although this is the most common example of weighted voting, this system has emerged in the world of politics as well, especially in the United States [2 ].
Today, the United States of America uses a weighted voting system in what most consider its most important election–the presidential election. Weighted voting entered mainstream American politics with the creation of the Electoral College in 1787. In the Electoral College system, each state is allotted a certain number of electors representative of the state’s congressional delegation. Essentially, the Electoral College acts as a weighted voting system to elect the President. There are 56 players: 50 states, the District of Columbia, three Nebraska congressional districts, and two Maine congressional districts. The number of electors assigned to each player acts as the player’s weight, and these weights vary as each state could have a different congressional delegation. The weights range from 1 (for individual congressional districts) to 55 (for California’s delegation), and the quota of 270 is the simple majority of the sum of the weights, 538 [3].
Clearly, the weighted voting system is implemented all over the world in differing organizations and governments. However, this system brings with it more interesting things to consider. Since the weights of players can be all different, a critical question arises. Who controls elections? This leads to the study of what a player’s power is in such a voting system. One of the most common ways to determine power is through the Banzhaf Power Index. A study of this index is essential to understanding weighted voting systems.
The Banzhaf Index of Power and Its Application in Historical Events
A key point we need to keep in mind when we are exploring the weighted voting system is that the weight of a player does not necessarily imply a player's power. For example, it is possible for a weighted voting system with all varying number of weights to come down to a one-person, one-vote situation in which case all players have the same power.[4] The power of a player in a weighted voting system can be roughly defined as the ability of the player to influence the final outcome. There are many ways to measure mathematically the power of a player in a weighted voting system. We will introduce a fairly common approach here: the Banzhaf power index.
In order to understand this concept, let's first give out some definitions in a weighted voting system :
- Coalition: A coalition is a collection of voters who agree to vote the same way on a measure. The number of members in this collection can range from no voters to all voters in the system. Since an empty set will make no practical sense, so we usually do not count it. Therefore, the total possible coalitions for a weighted voting system of N voters = 2N-1. Also note that coalition is somewhat similar to the concept of sets in mathematics, so we can denote a coalition with the grouping symbol { }. For instance, if there are two voters in the system: P1,P2. There are 3 possible coalitions in total: {P1} , {P2}, {P1, P2}.
- Winning Coalition: A coalition that can force the motion to pass. In the above example, if P1 has 5 votes, P2 has 3 otes, and the quota q of the system equals 6 (can be represented by {6: 5, 3}. Then the only possible winning coalition is {P1, P2}. Any other coalitions besides the winning ones are called losing coalitions.
- Critical Player: A player will be considered as a critical player if his or her withdrawal from the coalition will cause a winning coalition to become a losing coalition. For instance, in the above system {6: 5, 3}, {P1, P2} is the only winning coalition. If P1 withdraws, then P2 alone cannot reach the quota. Therefore, P1 is counted once as a critical player. Similarly, if P2 withdraws, then P1 alone cannot reach the quota and hence P2 is also counted once as a critical player.
- Banzhaf Power: The Banzhaf power of a voter is the total number of times he or she is a critical player in the coalitions. Then as shown above, P1 has a Banzhaf power = 1 (let's denote it as B1=1), and P2 has a Banzhaf power =1 (B2 = 1). The total number of time any player is critical = B1 + B2 = 2.
- Banzhaf Index: The Banzhaf index of a voter i is his or her Banzhaf power devided by total Banzhaf Power of the weighted voting system= Bi /Btotal .
Now it is time to talk about how the method of Banzhaf power index is carried out. The idea is that a player's power is quantified as the percentage of times that the player is a critical player. Here is a step-by-step guide on how to compute the Banzhaf power index for a Player Pi:
Step 1: Determine all winning coalitions.
Step 2: Identify critical players in each winning coalitions.
Step 3: Count the number of times being a critical player for each voter. Add them up to obtain the total Banzhaf power Btotal .
Step 4: Find the number of times Pi is critical, denoted as Bi .
Step 5: BPI(Pi)= Bi/Btotal .
The concept of Banzhaf Power Index itself is not complicated, but listing all winning coalitions can be quite frustrating since when the number of voters increases the number of possible coalitions increases unproportionally. Fortunately, we have computers now and we can use them to speed up our calculation process. Here is a good online Banzhaf Power Index Calculater written by Bruce Conrad and Dan Reich [5]. It is a fun hands-on model and you can experiment with it whenever you want.
Now we have learned how to caculate the Banzhaf power index, let's apply it to real life problems. An interesting example will be the first case where the Banzhaf power index was used in history. Banzhaf, the guy whom this power index was named after, wanted to prove that the Nassau County Board's voting system was unfair[6]. The voting system could be simplified as {16: 9, 9, 7, 3, 1, 1} and the six voters could be denoted as A-F.
Using emuneration we can find 32 winning coalitions and underline all critical players in each winning coalition:
AB, AC, BC
ABC, ABD, ABE, ABF, ACD, ACE, ACF, BCD, BCE, BCF
ABCD, ABCE, ABCF, ABDE, ABDF, ABEF, ACDE, ACDF, ACEF
BCDE, BCDF, BCEF
ABCDE, ABCDF, ABCEF, ABDEF, ACDEF, BCDEF
ABCDEF
Therefore, Btotal = 48, BA = BB = BC = 16, BD = BE = BF = 0. Hence BPIA = BPIB = BPIC = 1/3, while BPID = BPIE = BPIF = 0.
Proved by the Banzhaf Power Index, this voting system was clearly unfair because three of the voters had no power to swing the outcome at all, even though they were one fourth of the population.
We can also use this method to determine the power of provinces under Canadian Constitution. There are 159 winning coalitions under the Canadian Constitution. The result is calculated by computer so we are not going to show the process here. The final breakdown of the Banzhaf Index of Power is given in the table below: [7]
Canada: Power of Provinces under Canadian Constitution [7]
| |
Population | Percentage of Population | Seats in Parliament | Percents of Seats | The Banzhaf Power | Banzhaf Index |
|---|---|---|---|---|---|---|
| Ontario | 10,084,885 | 37.06% | 103 | 34.22% | 101 | 13% |
| Quebec | 6,895,963 | 25.34% | 75 | 24.92% | 85 | 11% |
| British Columbia | 3,282,061 | 12.06% | 34 | 11.30% | 81 | 11% |
| Alberta | 2,545,553 | 9.35% | 26 | 8.64% | 75 | 10% |
| Saskatchewan | 988,928 | 3.63% | 14 | 4.65% | 73 | 9% |
| Manitoba | 1,091,942 | 4.01% | 14 | 4.65% | 73 | 9% |
| New Brunswick | 723,900 | 2.66% | 10 | 3.32% | 71 | 9% |
| Nova Scotia | 899,942 | 3.31% | 11 | 3.65% | 71 | 9% |
| Prince Edward Island | 129,765 | 0.48% | 4 | 1.33% | 69 | 9% |
| Newfoundland | 568,474 | 2.09% | 7 | 2.33% | 71 | 9% |
| Yukon Territory | 27,797 | 0.10% | 1 | 0.33% | 0 | 0% |
| Northwest Territories | 57,649 | 0.21% | 2 | 0.66% | 0 | 0% |
| TOTAL | 27,211,413 | 100% | 301 | 100.00% | 770 | 100% |
As the table demonstrates, there are also two dummies who have no power at all, so the voting system is not fair. Then, what can be called an equal voting system? The next section will give you a hint on this problem.
Problems with Weighted Voting and Historical Events
Nowadays, social inequality is considered to be one of the biggest problems the modern society faces. Therefore, the majority of developed countries, especially the US launch programs and invest big amounts of money to fight with social inequality. However, what the US government forgets about is its own voting system. The United States of America uses weighted voting system in the presidential election. Considering the fact how important the principle of equality nowadays is, the use of weighted voting system in such a developed country is at least unexpected.
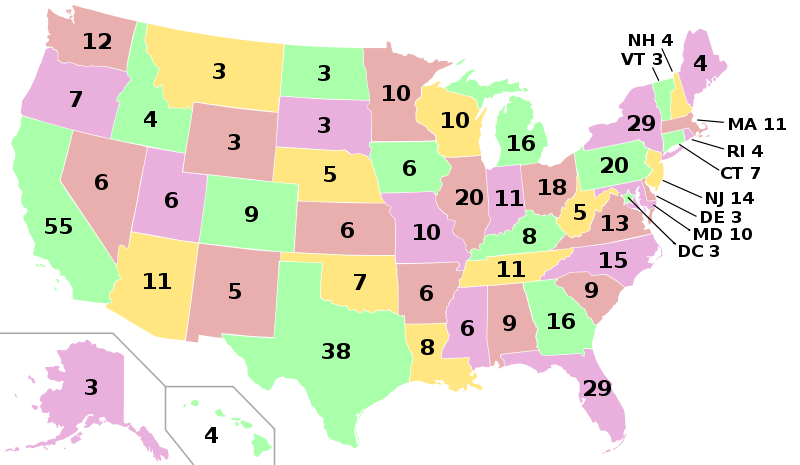
As it can be seen on the following image (Electoral college, 2012), states and District of Columbia represent players, while their electors act like weights.
The District of Columbia and all states, except Nebraska and Maine follow winner-takes-all rule [8]. According to the rule, candidate with the most votes gets all of the state's votes. Obviously winner-takes-all rule ignores the opinion of those who did not vote for the winning candidate, since their votes will not be considered afterwards. As a result, it can lead to the election in which the candidate with the most popular votes does not win the election, and it has already happened several times [9].
| Year | Most popular votes candidate |
Winner of the election | Votes for the most popular candidate | Votes for the election winner | Difference |
| 1824 | Andrew Jackson | John Q. Adams | 151 271 | 113 122 | 38 149 |
| 1876 | Samuel J. Tilden | Rutherford B. Hayes | 4 288 191 | 4 033 497 | 254 694 |
| 1888 | Grover Cleveland | Benjamin Harrison | 5 539 118 | 5 449 825 | 89 293 |
| 2000 | Al Gore | George W. Bush | 50 992 335 | 50 445 156 | 537 179 |
Obviously such elections ignore the majority opinion and violate the principle of equality, when all voters are equal. In other words, outcomes of these elections does not follow the basic principles of democracy and some people have much more power than others. To illustrate it let's examine elector's map again.
As it was mentioned before, to win the election, a candidate must recieve at least 270 of electoral votes. As a result, it is possible to win the election by winning in eleven states having the largest weights. California, Texas, New York, Florida, Pennsylvania, Illinois, Ohio, Georgia, Michigan, North Carolina, and New Jersey give 270 votes. According to population estimate, July1, 2012, these states have a population combined about 178,591,446, or 57.07% of total population of the United States (List of U.S. States and territories by population) [10]. Even though the population of these states exceeds the rest population of the US, all of these states follow winner-takes-all rule. Thereby, recieving 50.1% of votes in every of these states would still result in winning the presidential elections. In other words, even though it is highly unlikely but theoretically it is possible to win the presidential election by receving only 28.60% (57.07*0.501) of votes, assuming that amount of voters is proportional to the state's population. Thereby, less than the third of the total voters can decide the fate of the elections. For example, in the year of 2008, Barack Obama recieved 222 electoral votes by winning in 9 of 11 largest states, in other words, he recieved 82.22% of necessary votes in 9 states only [11].
So from the above analysis it is clear that people in different states have different power, in other words, they have different Banzhaf power index. So, according to the research conducted by Mark Livingston, in the year of 1990 every California voter had 3.3 more power to choose the President than any Montana voter [12].
For all the reasons above it is obvious that in some cases weighted voting system in the United States presidential elections can violate principles of democracy and equality and thereby, can not always be considered fair. Obviously, weighted voting system is not the best option for presidential elections in a democratic, equal society. In addition, as George C. Edwards stated in the year of 2011, "The United States is the only country that elects a politically powerful president via an electoral college and the only one in which a candidate can become president without having obtained the highest number of votes in the sole or final round of popular voting." [13]
Conclusion
Equality of rights has become one of the main principles of democracy. Therefore, equal voting is so important for the modern society. However, the principle of one person-one vote is not always fair. As it was mentioned before, in some cases some people should have different power because of their differing contributions, in these cases weighted voting system is usually used. However, this system is more complex than equal voting system, since as it was shown a player's weight is usually not his or her power. Therefore, in order to find true power players hold, people use different techniques including Banzhaf power index. Despite the fact that equality is usually taken for granted in the modern society, weighted voting system is very common, for example, in business members of board of directors of a shaholding company have weights proportional to the amount of shares they hold. Shareholding companies are not the only organizations using weighted voting system, the United States government also uses this system to elect the president. However, in this case, weighted voting system creates some problems including unintentional inequality and endanger democracy principles. Therefore, people should carefully choose which system to use in each particular case.
Bibliography
[1] Weighted Voting
[2] Penn State Weighted Voting Powerpoint
[3] World Bank Organizational Information
[4] Weighted Voting Systems
[5] Banzhaf Power Index Calculator by Bruce Conrad and Dan Reich
[6] Banzhaf, John F. (1965), "Weighted voting doesn't work: A mathematical analysis", Rutgers Law Review 19 (2): 317–343
[7] IU weighted voting
[8] U. S. Electoral College: FAQ
[9]10 of the closest presidential elections in United States history
[10] List of U.S. States and territories by population.
[11] Election center 2008
[12] Mark Livingstone, Banzhaf power index
[13] Edwards III, George C. (2011). Why the Electoral College is Bad for America (Second edition ed.). New Haven and London: Yale University Press. pp. 1, 37, 61, 176–7, 193–4