Applications

These incredibly complicated mathematical concepts have equally incredibly important uses. Primarily, Riemann Surfaces have become the natural way for mathematicians to observe multivalued functions. These are functions where a single input value can have multiple output values, or where one input value may produce a complex output value. This is most easily observed in the function:

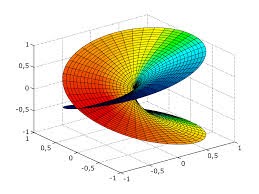
When x < 0, y has complex values, and for all real y-values, there are two possible x input values, ±x. The Riemann Surface for this function has two branches, one that moves from the self-intersection at zero in the positive direction, and one that moves in the negative. Notice in the image below, that starting at 0 on the right axis, there are two paths that can be taken to get to 1, going up or doing down. This visualization shows that both -1 and 1 are valid options to square to get a result of 1. Since we typically only view this function in two dimensions, we look at it top down, and miss the whole lower part of the function below zero.

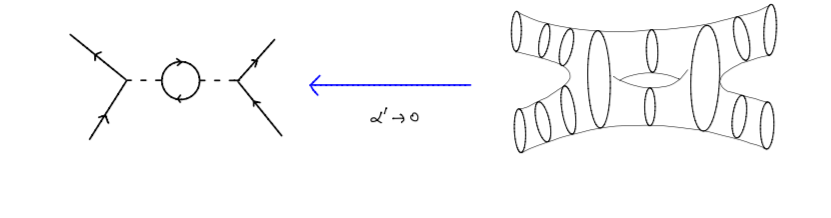
In terms of applications outside of mathematics, there are theories surrounding the idea that Riemann Surfaces may be a way to describe what are called “world sheets” in String Theory. A world sheet, noted as Σ_g, is the summation of all the strings in a local area of space-time. In other words, local bundles of string, when you look at them locally, form a sheet on a surface. This surface is often characterized as a Riemann Surface, especially the aforementioned hyperelliptic curves. String Theory is based around the idea that matter is made up of tiny strings that vibrate, giving the appearance of matter as we see it on earth. This gives rise to Riemann Surfaces as the strings are supposedly connected in long complex strings that vibrate to form the surfaces that appear as Riemann Surfaces. The way the strings “swing” around as they vibrate form the “sheets”. These tiny local sheets are then added up to become the world sheets. So,

when all the world sheets are put together, as mentioned before, they appear to form a Riemann Surface. The theory also goes on to explain that when the strings vibrate, their amplitude will only go so far, giving rise to the “holes” in these surfaces such as the genus in a torus (seen in the image above (Ried-Edwards, 2020)). The line picture on the left represents the strings and the picture on the right is what happens when these strings vibrate. The picture on the right appears to look like a torus, which is a Riemann Surface. Just like how when computing with Riemann surfaces, a map is used between the 2-dimensional string and the surface when relating the string’s frequency and mode (which is the number of nodes or sections in the wave of the string as it vibrates) to the surface it forms. This is just one theory in physics that utilizes Riemann Surfaces.