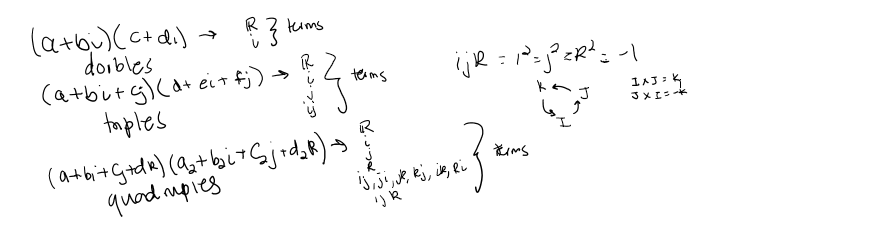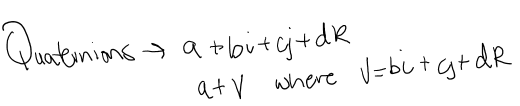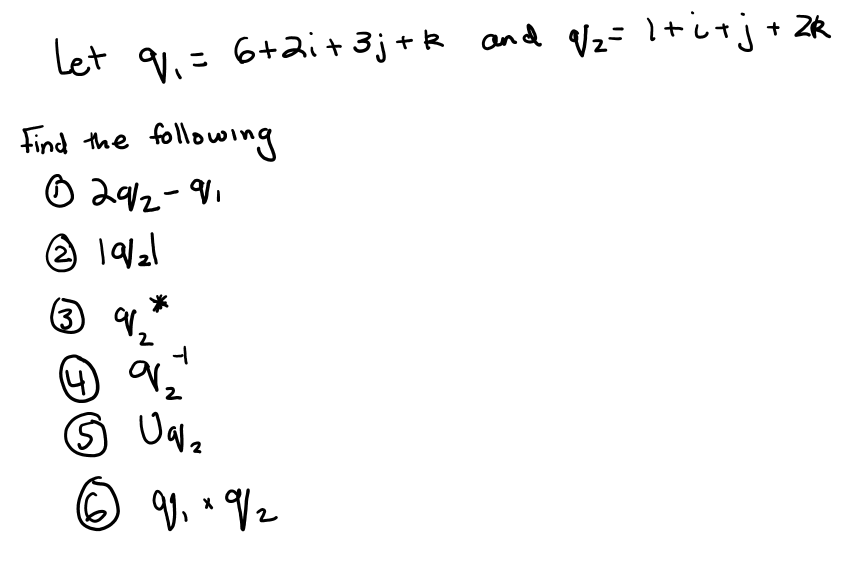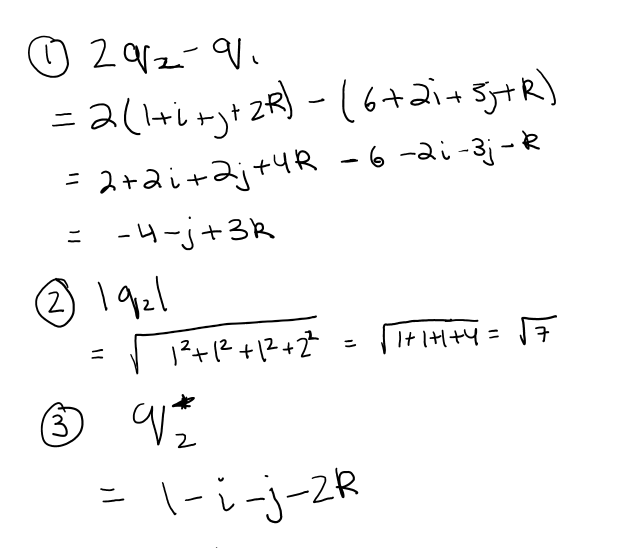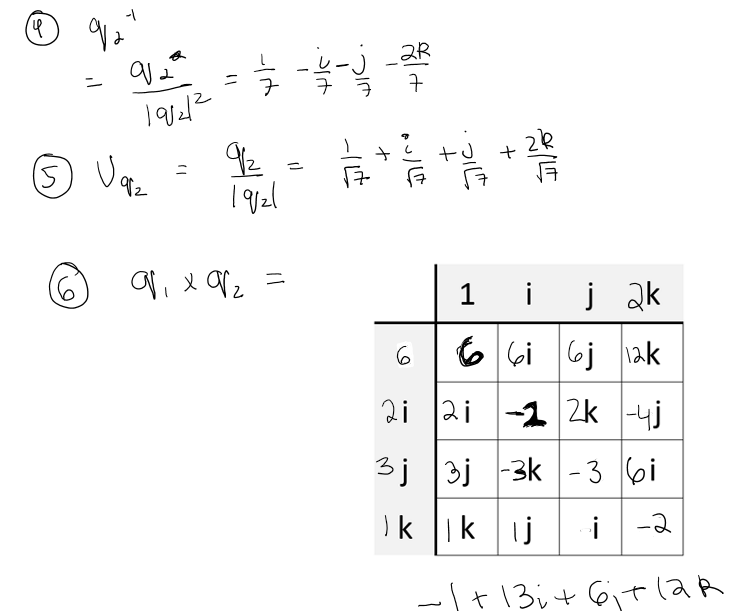Walther MA271 Fall2020 topic28 - Rhea

Quaternions

Author: Krish Gupta

What are quaternions? Who found quaternions? How and why were they developed? Do quaternions have an actual use? These are probably a few of the many questions you have regarding quaternions that prompted you to this paper. This paper will include a brief history of quaternions and their development, a longer discussion behind the motivation and development of quaternions along with a discussion on the applications of quaternions. Extended readings and further discussion resources will be provided for math enthusiasts to explore!

To boil it down to a single sentence: Quaternions are a number system that extend the complex number system into 3 dimensions and are extremely useful to model situations that require rotations or knowledge of the orientation of an object. A lot of quaternion algebra involves vector algebra. The quaternion product actually compromises of a dot, a scalar and a cross product. One will notice many similarities between how we calculate quantities with vectors and quaternions.

Before we dive into quaternions, knowledge of complex numbers and basic vector algebra is assumed to be mastered. Let’s define and review some concepts:

Complex Numbers - An extension of the real number system that has a real part and an imaginary part.

Cross Product - A product of two vectors that can be solved using determinants, and outputs a vector perpendicular to the original vectors.

Dot Product - A product of two vectors that can be calculated by summing the product of corresponding entries and outputs a scalar.

Euler’s Formula - A very important formula that relates trigonometric functions and exponential functions.

Quaternions are tough to visualize as they require being able to imagine a 4th dimension or at least being able to work with an extra parameter in 3D, rotations. We will look at why quaternions can model rotations and we will discuss some basic steps of quaternion algebra. But hopefully this paper will give you an essence of what quaternions are, how to work with them, where they came from and what they are for.

History

Every professional wishes to have that one monumental light bulb moment in his or her life. That split second when an academic is stuck on a problem but has a sudden insight that launches him/her into fame. Perhaps such epiphanies and light bulb moments are more dramatized by films and are less common in real life. But the discovery or perhaps the development of quaternions has a remarkable light bulb moment and a thrilling story that almost sounds like the plot of a movie.

An Irish man in the 1840s named William Rowan Hamilton wanted to extend the complex number system to a higher dimension. Hamilton was aware of complex numbers and the fact that you can use complex numbers to model a rotation in two dimensions using Euler’s Formula. Hamilton was also aware of the work of Olinde Rodrigues, another mathematician who worked on transformation groups.

But Hamilton had much trouble extending the complex system to three dimensions. In one of his books Hamilton wrote how his brother would always ask him every morning, "Well, Papa, can you multiply triples?" But he always had a pessimistic reply, "No, I can only add and subtract them." Later that year, Hamilton and his better half were taking a walk along the Royal Canal in Dublin. As they were walking across a bridge, the answer to the puzzle suddenly came to Hamilton. He has his light bulb moment just like the movies. He realized that one could not perhaps easily multiply or divide triples, but he could do so with quadruples. He realized he could use 3 of the numbers in the quadruple to specify a specific point, further validating his system. Just when Hamilton was struck with this sudden knowledge, he grabbed a rock near him on the bridge and carved on it the multiplication identity that allows quaternion multiplication. The image below is of the rock that is still there in memory of Hamilton's discovery.

To this day one can visit Ireland and see the rock on the bridge where quaternions were born. In fact, in Hamilton’s honor there is a parade every year through the bridge on October 16.

Quaternions were a hot topic in the 1840s when Hamilton discovered them. But for the next 150 years they were mostly a mathematical curiosity. It was not until the late 20th century that we found widespread applied uses of Quaternions. Hence, it would not be a stretch to say that quaternions is a field of mathematics that has had a recent rebirth.

Main Discussion

Imagine a tiny sphere located on the y axis. If we try to rotate this sphere 90 degrees around the x-axis it will land on the z axis. If we now try to rotate this sphere on the z axis 90 degrees around the y-axis it will now be on the x axis. But let’s say we switch the order of rotations. If we rotate a sphere on the y axis about the y-axis, it does not move. If we then rotate it by the x axis it lands on the z-axis. This is a stark discovery. Rotating an object in an xy orientation vs yx orientation produced significantly different results. So the fact that rotations are not commutative is what makes them so unique. One way we can use to model these rotations is a rotation matrix but we will discuss later how rotation matrices are not always reliable as they are susceptible to a situation named Gimbal Lock, where when 2 of our 3 axes align, we lose a degree of freedom. So we need a system that circumvents Gimbal Lock and is able to capture the non-commutativity of rotations.

Complex number system is one such system where we can model rotating a point in two dimensions. Using Euler’s formula we can convert a point to a rotation of a segment. Hamilton’s goal was to do exactly what Euler did but in a higher dimension.

In one dimension

Rotating an object in one dimension does not change the position of the object but might change its orientation. You can imagine rotating a tennis ball pinned to the center of a broom stick. It just rotates in position without change in translational location.

In two dimensions

We can use Euler’s formula to model rotations in 2D. With cosine and sine functions and theta as our parameter, we can rotate a point, P by some angle theta in some V direction.

Let (1,0) be the point P. If we rotate P 90 degrees, with positive angles defined in the counterclockwise direction, we get (0,1) and rotating it 90 more degrees gives us (-1,0). One will notice how these rotations we have described just rotates the unit vector in the direction of the x axis around the unit circle. One can think of all points on the unit circle as rotations of the unit vector of the x-axis.

In three dimensions

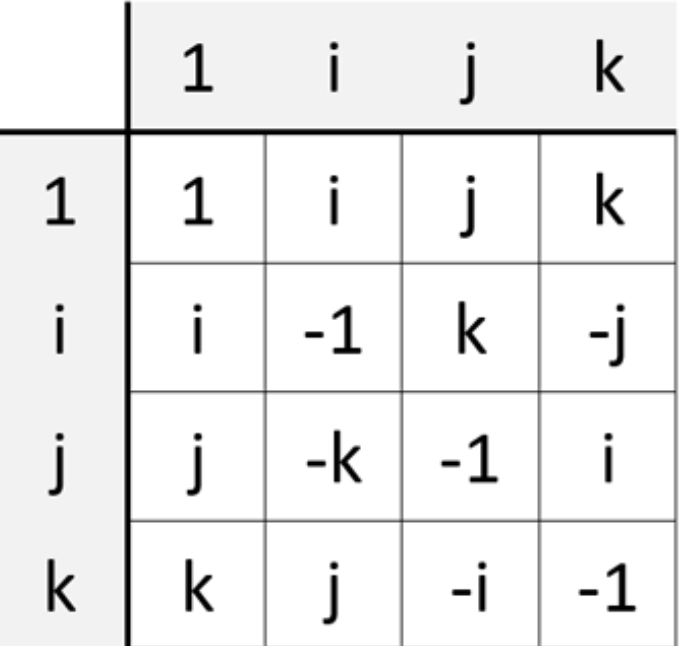
We can see below how multiplication worked easily with doubles in 2D. But multiplying triples (doubles with an extra parameter of j) gave an "ij" term which simply did not make sense to Hamilton. So he added another parameter, k, to solve this problem. He realized that any two of i,j or k multiplied could give you the 3rd and i*j*k =1. But we need to remember quaternions are non-commutative. So i*j and j*i are different by a factor of a minus sign. To figure our multiplication of these imaginary parameters we can use a ring of ijk where going counterclockwise gives you a positive answer but going clockwise gives you a negative one (same convention as physics).

So then we can write a quaternion with the 4 parts as the following. But for ease we can write a quaternion in two parts with a being the real part and V representing the vector part.

Below are the following properties of quaternion arithmetic. Addition, subtraction and scaling quaternions is fairly simple. Multiplying is a longer and tedious process. We have a formula involving cross and dot products to calculate a product but it is also easier to calculate using the table and summing the real parts and i's and j's and k's.

There are some other quantities we can calculate with quaternions. Norm is an important quantity to know the length of a quaternion and inverse is an important quantity to use for quaternion division.

There is also something called unit quaternions. A unit quaternion is a quaternion of length 1. We can find the unit quaternion by dividing the quaternion by its magnitude just like we find a unit vector. Unit quaternions are notated as Uq and are extremely useful in quaternions because multiplying unit quaternion produces a unit quaternion.

Below are some following numerical examples to enhance your understanding and to strengthen your calculating abilities when it comes to quaternions.

Applications

Theoretical mathematics is an academic's pleasure. A mathematician loves analysis and abstract algebra more than anything. But it is amazing to see the wonders of mathematics when applied to the real world. Quaternions have lived both lives for most of the 19th and 20th century quaternions had theoretical attributes. However, at the dusk of the 20th century but even more at the dawn of the 21st century, we saw real world applications of Quaternions. A lot of them employ the fact that quaternions can be used to model rotations.

Aeronautics is a major new prospect for use of quaternions. Orientation is a big part of flight. When aerospace was gaining traction, many were worried about the preciseness of mathematics needed to execute these missions to the accuracy that they require. Gimbal lock is a major problem in this field. Gimbal Lock refers to a common problem in 3D where modeling becomes hard when 2 of your 3 axes align and are basically the same because then you lose a degree of freedom. When using other methods to model rotations like matrices, these problems exist but if quaternions are used we can completely avoid Gimbal Lock.

The image below shows normal orientation versus Gimbal lock.

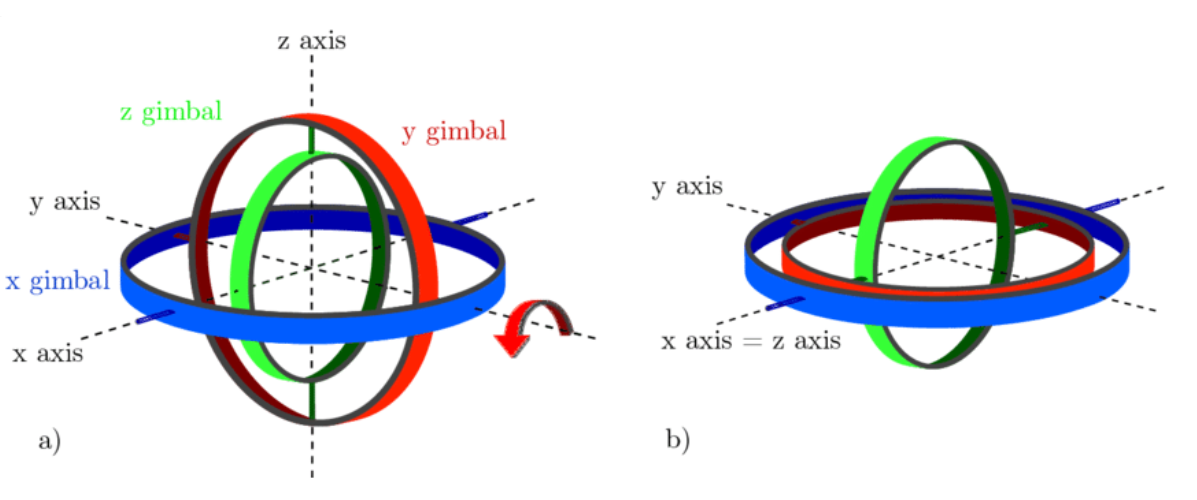
Robotics is also a major application of quaternions. In fact, we can map the rise of robotics and the comeback of quaternions and we will notice that they follow a very similar trend. Robots also need to worry about rotation and orientation. Simple and crude robots only have the ability to move translationally. But with state of the art technology and public demand, there is a dire need to improve our robots and make them even more advanced. Quaternions again allow to circumvent the Gimbal Lock but also are a better and more compact method of storing data than rotation matrices.

Physics in general including quantum mechanics and electromagnetisms have found ways to utilize quaternions to make processes simpler. In fact both Maxwell in his work on electromagnetism and Heisenberg on his work of modern physics wrote and used quaternions in their work. Many scientists and mathematicians were a big fan of quaternions because it compressed their notation a lot and made it much simpler than using matrices or other methods.

Overall, quaternions have many more uses than we have discussed here. Many articles say that phones and electric toothbrushes use quaternions all the time. Anything that has to do with orientation and collecting data on the orientation of something like a rocket or a mobile tablet employs quaternions in one form or another. So while quaternions might have been a mathematical curiosity 150 years ago, now they have many real world applications and are changing the world, one rotation at a time.