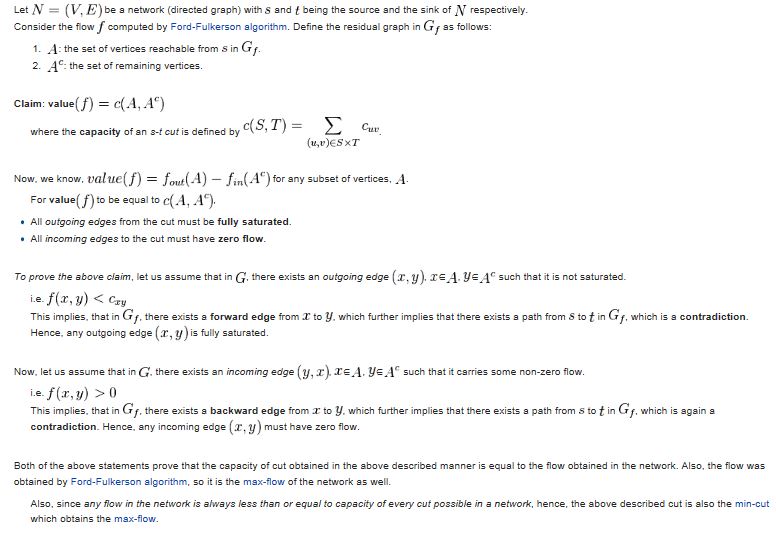What is a flow in a graph? What is a cut? How do they relate? Describe some ideas around these two concepts.
Flows and Cuts in Graphs
What is a flow in a graph?
Useful in coding, flow graph is a visual representation of the various paths the code of a computer program can take. Flow in a graph is depicted using a series of arrows and nodes that display the route one can travel to each node. Each node represents a particular line of code in a program.
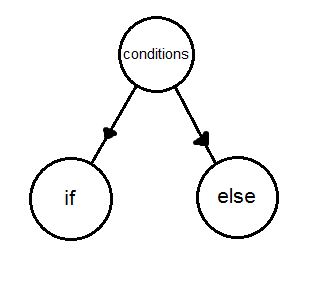
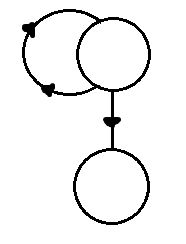
This can be properly illustrated in code by using if statements and loops. An if-else statement would result in a multiple edges branching out of a single node. A loop would result in just that, a loop. Depending on whether certain conditions are met, the loop may go for a certain number of iterations before executing the next block of code.
If-Else Control Flow Graph Loop Control Flow Graph
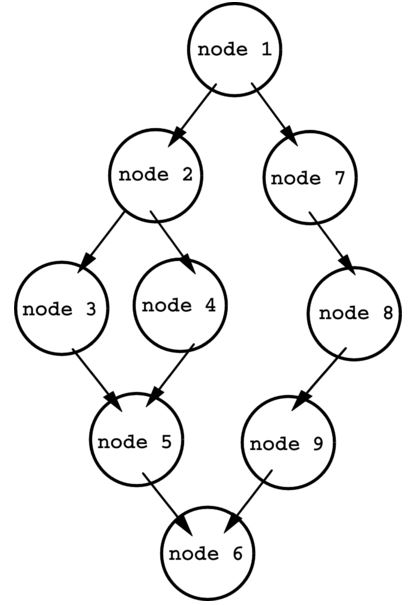
Below is another simple example of a flow graph:
- Node 1 is the initial line of code.
- Depending on the outcome of node 1, the code will flow ether to node 2 or node 7.
- The code will continue until the flow has reached the destination node (i.e. node 6), following the flow of the graph throughout.
Retrieved from https://www.owasp.org/index.php/Static_Code_Analysis
Why use a flow graph?
- To determine the usefulness of the parts of a program. A node without an arrow directed towards it may be deleted. This is often called dead code.
- To identify and isolate problems such as infinite loops, where program execution does not move beyond a single node. For various reasons, a block of code may cycle indefinitely.
- To help create a program dependence graph. This type of graph shows what areas of a program are reliant on other parts, and if the code is running in the correct sequence.
[1]
What Is A Cut?
Definition
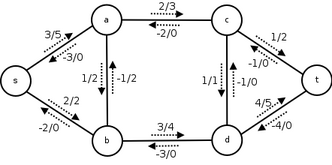
A cut is a partition of a graph. The cut-set of a cut is the set . The size of a cut is the number of edges in the cut-set. If the edges are weighted, the value (or weight) of the cut is the sum of the weights. A bond is a cut-set that does not have any other cut-set as a proper subset.
In graph theory, a cut is a partition of the vertices of a graph in which the capacities are complimentary of one another. In other words, if an edge has met its capacity, then there is a possible cut in the graph. The cut-set of the cut is the set of edges whose end points are in different subsets of the partition. Edges are said to be crossing the cut if they are in its cut-set.
In an unweighted undirected graph, the size or weight of a cut is the number of edges crossing the cut. In a weighted graph, the same term is defined by the sum of the weights of the edges crossing the cut.
In a flow graph, an s-t cut is a cut that requires the source and the sink to be in different subsets, and its cut-set only consists of edges going from the source's side to the sink's side. The capacity of an s-t cut is defined as the sum of capacity of each edge in the cut-set.
Minimum Cut and Maximum Cut
A cut is minimum if the size of the cut is not larger than the size of any other cut. The max-flow min-cut theorem proves that the maximum network flow and the sum of the cut-edge weights of any minimum cut that separates the source and the sink are equal. There are polynomial-time methods to solve the min-cut problem, namely the Edmonds-Karp algorithm.
Conversely, a cut is maximum if the size of the cut is not smaller than the size of any other cut.
Note that min-cut and max-cut are not dual problems in the linear programming sense, even though one gets from one problem to other by changing min to max in the objective function. The max-flow problem is the dual of the min-cut problem.
Retrieved from http://en.wikipedia.org/wiki/Flow_network
Cut space
The family of all cut sets of an undirected graph where there is no more room for an expansion in capacity is known as the cut space of the graph. If the edges of the graph are given positive weights, the minimum capacity of the cut space can be described by a tree on the same vertex set as the graph.e. Each edge of this tree is related to a bond in the original graph, and the minimum cut between two nodes s and t is the minimum capacity among the ones related with the path from s to t in the tree.
[2]
How Do They Relate?
In simple terms, we will get:
MAX FLOW = MIN CUT
Here is a proof from Eugene Lawler to explain this concept...
Retrieved from http://en.wikipedia.org/wiki/Max-flow_min-cut_theorem
[3]
In order to get a hands on approach, here is another example from youtube, http://www.youtube.com/watch?v=7jFoyLk2VjM
How To Apply This Concept
- In computer coding, this concept of flow in a graph is very similar to an "if statement". The next step is directly correlated to the result of the preceding step in order to reach its final destination.
- Cuts in a graph will show where more substance can be added, or where improvements can be made in order to make the flow larger.
References
[1] http://www.wisegeek.com/what-is-a-control-flow-graph.htm
[2] http://en.wikipedia.org/wiki/Cut_(graph_theory)
[3] Eugene Lawler (2001). "4.5. Combinatorial Implications of Max-Flow Min-Cut Theorem, 4.6. Linear Programming Interpretation of Max-Flow Min-Cut Theorem". Combinatorial Optimization: Networks and Matroids. Dover. pp. 117–120. ISBN 0-486-41453-1.