What is a "polynomial time algorithm", and what isn't? Is there a difference? What do we know about these two concepts?
Contents
[hide]- 1 What is this P vs NP?
- 1.1 You may have heard about a problem called the P vs NP Problem. It's a problem that falls under both Computer Science and Mathematics, particularly a field called Theoretical Computer Science. The subject is part of Computational Complexity Theory. It's practically the study of computing and consequently its resources (such as time it takes to compute, the space/RAM, and power consumption). If I haven't made out how big of a deal this problem is; beginning 2000, there are seven major math problems selected by the Clay Mathematics Institute which are called the Millennium Problems. Well, it so happens that this P vs NP problem is one of those seven major math problems and the first solution to the P vs NP problem is a guaranteed US $1,000,000 from the Clay Mathematics Institute. Oh and did I mention that only ONE problem has been solved so far... But I still haven't answered the question: WHAT IS P VS. NP? . . . SO LET'S DIVE IN . . . Time Complexity
- 1.2 What is the difference between P and NP?
- 1.3 NP-Hard and NP-Complete
- 1.4 History
What is this P vs NP?
You may have heard about a problem called the P vs NP Problem. It's a problem that falls under both Computer Science and Mathematics, particularly
a field called Theoretical Computer Science.
The subject is part of Computational Complexity Theory. It's practically the study of computing and consequently its resources (such as time it takes to compute, the space/RAM, and power consumption).
If I haven't made out how big of a deal this problem is; beginning 2000, there are seven major math problems selected by the Clay Mathematics Institute which are called the Millennium Problems.
Well, it so happens that this P vs NP problem is one of those seven major math problems and the first solution to the P vs NP problem is a guaranteed US $1,000,000 from the Clay Mathematics Institute.
Oh and did I mention that only ONE problem has been solved so far...
But I still haven't answered the question: WHAT IS P VS. NP?
.
.
.
SO LET'S DIVE IN
.
.
.
Time Complexity
We begin with time complexity.
Time complexity is basically the amount of time that an algorithm needs to run to give a final output or solution.
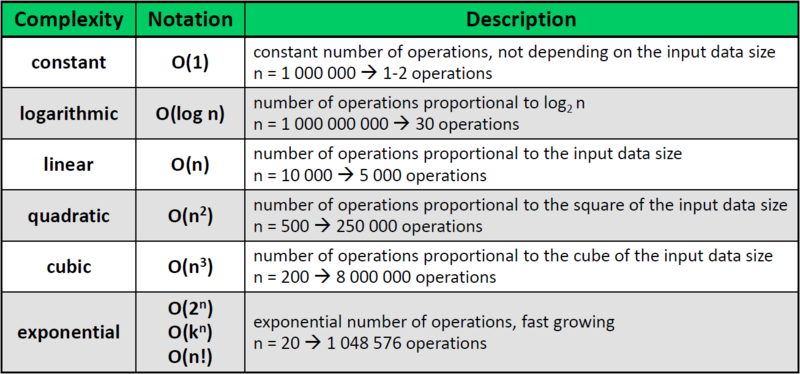
So let's take a large number and run through each number. So for example, 1,000,000,000,000 would take 12 steps to get through. The time to do this is denoted by a big O and in this case, the big O is followed by a one: O(1) to represent that it is a constant time problem.
Next let us take two large numbers; let's say the number 1,000,000 where there's 7 digits which we denote with n=7 (which we'll call the sample size) and the number 2,000,000 with n=7.
We add them:
1,000,000
+2,000,000
3,000,000
That is considered Linear time denoted by O(n).
Now let's multiply two numbers: 23 with n=2 and 37 with n=2
We multiply: 23
37
161
+690
851
This is consider Polynomial time denoted in this instance O($ n^2 $). In general polynomial time is denoted O($ n^k $) where k>1.
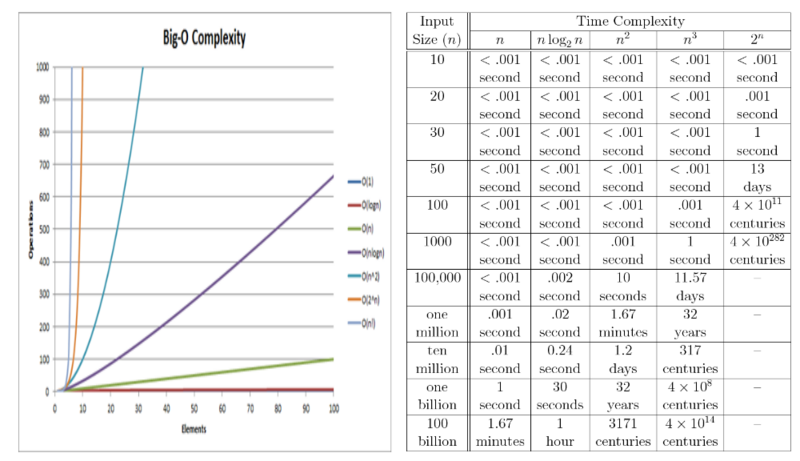
We can continue down with complexity and larger times. The graphs below demonstrates different computational time steps.
As you can see, the time to calculate the solution becomes longer and longer. So linear time is about the fastest way to compute an answer where polynomial time is very manageable time a computer needs to process a problem.
What is the difference between P and NP?
P stands for “polynomial time”. This the subset of problems that can be guaranteed to be solved in a polynomial amount of time related to their input length. Problems in P commonly operate on single inputs, lists, or matrices, and can occasionally apply to graphs. The typical types of operations they perform are mathematical operators, sorting, finding minimum and maximum values, determinates, and many others.
Some examples of problems in P are:
Name
Complexity
Description
Array Indexing
$ O(1) $
Selecting an element in an array
Binary Search
$ O(log(n)) $
Searching through a sorted list of values by starting in the middle and eliminating half of the remaining values at each iteration.
Variable Length Addition
$ O(n) $
Addition used in many scripting languages such as Python or MATLAB
Variable Length Subtraction
$ O(n) $
Subtraction used in many scripting languages such as Python or MATLAB
Variable Length Multiplication
$ O(n) $
Multiplication used in many scripting languages such as Python or MATLAB
Quicksort
$ O(n log(n)) $
Generic sorting algorithm
Mergesort
$ O(n log(n)) $
Generic sorting algorithm
Heapsort
$ O(n log(n)) $
Generic sorting algorithm
Dijkstra's Shortest Path Algorithm
$ O(|V|^2) $ for dense graphs.
Finding the shortest path from point a to point z through a graph with weighted edges.
AKS Primality Test
$ O(log(n)^{12}) $
A test to see whether a number is prime or composite. This is an interesting case of a problem that was not known to be in P until 2002.
NP stands for “nondeterministic polynomial time”. These problems are ones that can be solved in polynomial time using a nondeterministic computer. This concept is a little harder to understand, so another definition that is a consequence of the first is often used. NP problems are problems that can be checked, or “certified”, in polynomial time. The output of an NP solving program is called a certificate, and the polynomial time program that checks the certificate for its validity is called the certification program.
Problems in NP commonly involve graphs.
Some examples of NP problems are:
Name
Type
Description
Boolean Satisfiability (SAT)
NP-Complete
This is the question, does my Boolean expression have any input that will cause a “true” output. This is also the basis for the NP-Complete subset of NP.
Clique Problem
NP-Complete
Given graph G and a natural number k, is there a subset H of size k that is complete?
Graph Coloring
NP-Complete
Given graph G and k colors, output a coloring of G such that no two adjacent vertices share the same color.
Minesweeper
NP-Complete
See below
Travelling Salesman Problem
NP-Complete
Given a graph of cities and weighted edges between them, what is the shortest cycle to both start and end at the same city while visiting every other city exactly once?
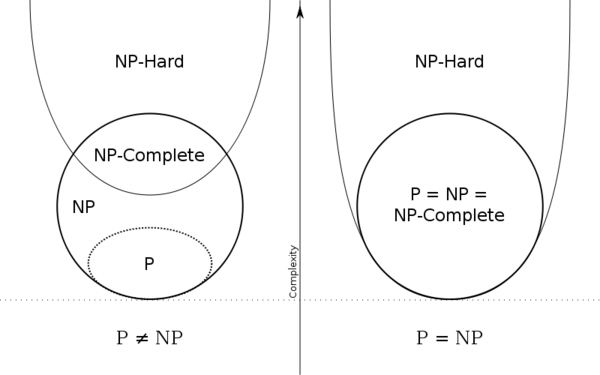
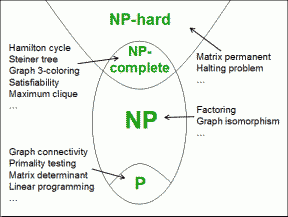
NP-Hard and NP-Complete
NP-hard:
A problem is NP-hard if it as least as hard as the hardest problems known to be NP. This leads to two possibilities: either the problem is in NP and also considered NP-hard, or it is more difficult than any NP problem.
NP-complete:
This classification is the intersection of NP and NP-hard. If a problem is in NP and also NP-hard, then it is considered NP-complete. This class of problems is arguably the most interesting for its consequences on many other types of problems.
This image from Wikipedia: NP-Hard shows the relation between P, NP, NP-Hard, and NP-Complete.
Minesweeper Problem:
Many people are familiar with the seemingly simple computer game Minesweeper, in which the player clicks locations on the board to reveal numbers, and the numbers correspond to the number of adjacent squares (including corners) that contain mines. Once the player has clicked every square that does not contain a mine, the player wins. If the player clicks a square with a mine, the player loses.
From this concept, an NP-complete problem arises. If a picture of a game in progress is given, determine whether or not a gameboard could be generated to fit the scenario shown.
The first picture below shows a game in progress, with 4 mines correctly flagged, many squares correctly labelled, and many squares yet uncovered.

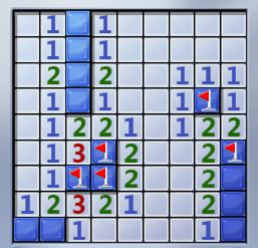

Because I actually played this game (and won), I know that it a solution to the problem did exist. And for a board of this size, it would be relatively simple to find out. But for an m-by-n board, it would not be so simple a question. In order to determine if a solution exists, one must either
1.
Check all possible mine arrangements and check to see if the board picture given fits correctly, or
2.
Correctly guess for each square whether or not there is a mine, eventually filling in the entire board.
Because the second strategy above is valid (if one could correctly guess on every square), the problem is considered NP, and the question could be answered in linear time with the number of squared yet uncovered. However, a deterministic machine could only guess correctly every time in the best case, and the hardness of problems is determined by the worst case.
The second a third pictures illustrate the solution to the game, proving that in this case, the board shown in the first picture was actually valid.
History
To show how difficult this problem is to solve, check out this list of attempted proofs to the problem:
History of P=NP Proofs
Evaluation of the permanent begins with Binet and Cauchy in 1812. Despite many attempts, an efficient algorithm for general matrices has proved elusive. After that, a notable breakthrough happened about 40 years ago with the publication of Kasteleyn’s algorithm for counting perfect matching in planar graphs by using O(n3) arithmetic operations in 1961. Then in 1979 Valiant proved that exact computation of the permanent is P-complete, and hence not possible in polynomial time. Since then the focus has shifted to efficient approximation algorithms with precise performance guarantees.
As shown in the graph below, linear programming problems were part of NP and invented by American mathematician George Dantzig in 1947. Linear programming is a method to achieve the best outcome and grows exponentially with the size of the input. However, a polynomial time algorithm with computational steps grows as a power of the number of variables, rather than exponentially was discovered by Russian mathematician Leonid Khachian in 1979. Therefore, he proved that linear programming problems are actually P. Then in 1971 American computer scientist Stephen Cook proved that the satisfy problem is NP-complete, which was the first problem shown to be NP-complete. These discoveries also opened the way to showing other problems are NP-complete problems. In 2000 American mathematician Stephen Smale devised the P vs NP problem.
A theoretical computer mathematician makes THE breakthrough. At first he is overjoyed at his success.
He tests it on the factorization problem and he breaks apart a billion sized number into its factors in mere minutes that would have taken centuries of supercomputer power to solve.
After the excitement wears off, the stark reality of what he now has sinks in.
In his hands lies the key to most of data encryption, the solution to many of scientific problems, optimization of routes such as for market strategies and lest we forget, a $1,000,000 prize from Clay Institute.
Like any human, curiosity gets the best of him and he wanted to test out the full power of his solution. He goes to Wallstreet and in the middle of the a major trade, he easily hacks right through the RSA encryption security and transfers some of the money to a bank account in Switzerland he previously just set up.
He instantly regrets his action, fearing legal reprecutions but none come. Plagued with guilt, he makes good of his stolen money and opens a scientific oriented company to solve major problems in biochemistry, physics, and economics.
Here's problems he manages to solve:
- Biochemistry: Protein and enzyme folding for cures
- Physics: the many body problem and chaotic systems
- Economics: Ideal routes to save on time and gas
Check-Out the Travelling Salesman 2012 Movie Info: http://www.imdb.com/title/tt1801123/
Authors:
Jason Kohl (kohl@purdue.edu)
Cameron Young (young149@purdue.edu)
Patrick Kelley (kelley28@purdue.edu)
Intae Whoang (iwhoang@purdue.edu)
Qingshi Zhou(zhou133@purdue.edu)
.
.
.
SO LET'S DIVE IN
.
.
.
Time Complexity
We begin with time complexity.
Time complexity is basically the amount of time that an algorithm needs to run to give a final output or solution.
So let's take a large number and run through each number. So for example, 1,000,000,000,000 would take 12 steps to get through. The time to do this is denoted by a big O and in this case, the big O is followed by a one: O(1) to represent that it is a constant time problem.
Next let us take two large numbers; let's say the number 1,000,000 where there's 7 digits which we denote with n=7 (which we'll call the sample size) and the number 2,000,000 with n=7.
We add them:
+2,000,000
3,000,000
That is considered Linear time denoted by O(n).
Now let's multiply two numbers: 23 with n=2 and 37 with n=2
We multiply:37
161
+690
851
This is consider Polynomial time denoted in this instance O($ n^2 $). In general polynomial time is denoted O($ n^k $) where k>1.
We can continue down with complexity and larger times. The graphs below demonstrates different computational time steps.
As you can see, the time to calculate the solution becomes longer and longer. So linear time is about the fastest way to compute an answer where polynomial time is very manageable time a computer needs to process a problem.
What is the difference between P and NP?
P stands for “polynomial time”. This the subset of problems that can be guaranteed to be solved in a polynomial amount of time related to their input length. Problems in P commonly operate on single inputs, lists, or matrices, and can occasionally apply to graphs. The typical types of operations they perform are mathematical operators, sorting, finding minimum and maximum values, determinates, and many others.
Some examples of problems in P are:
| Name | Complexity | Description |
|---|---|---|
| Array Indexing | $ O(1) $ | Selecting an element in an array |
| Binary Search | $ O(log(n)) $ | Searching through a sorted list of values by starting in the middle and eliminating half of the remaining values at each iteration. |
| Variable Length Addition | $ O(n) $ | Addition used in many scripting languages such as Python or MATLAB |
| Variable Length Subtraction | $ O(n) $ | Subtraction used in many scripting languages such as Python or MATLAB |
| Variable Length Multiplication | $ O(n) $ | Multiplication used in many scripting languages such as Python or MATLAB |
| Quicksort | $ O(n log(n)) $ | Generic sorting algorithm |
| Mergesort | $ O(n log(n)) $ | Generic sorting algorithm |
| Heapsort | $ O(n log(n)) $ | Generic sorting algorithm |
| Dijkstra's Shortest Path Algorithm | $ O(|V|^2) $ for dense graphs. | Finding the shortest path from point a to point z through a graph with weighted edges. |
| AKS Primality Test | $ O(log(n)^{12}) $ | A test to see whether a number is prime or composite. This is an interesting case of a problem that was not known to be in P until 2002. |
NP stands for “nondeterministic polynomial time”. These problems are ones that can be solved in polynomial time using a nondeterministic computer. This concept is a little harder to understand, so another definition that is a consequence of the first is often used. NP problems are problems that can be checked, or “certified”, in polynomial time. The output of an NP solving program is called a certificate, and the polynomial time program that checks the certificate for its validity is called the certification program.
Problems in NP commonly involve graphs.
Some examples of NP problems are:
| Name | Type | Description |
|---|---|---|
| Boolean Satisfiability (SAT) | NP-Complete | This is the question, does my Boolean expression have any input that will cause a “true” output. This is also the basis for the NP-Complete subset of NP. |
| Clique Problem | NP-Complete | Given graph G and a natural number k, is there a subset H of size k that is complete? |
| Graph Coloring | NP-Complete | Given graph G and k colors, output a coloring of G such that no two adjacent vertices share the same color. |
| Minesweeper | NP-Complete | See below |
| Travelling Salesman Problem | NP-Complete | Given a graph of cities and weighted edges between them, what is the shortest cycle to both start and end at the same city while visiting every other city exactly once? |
NP-Hard and NP-Complete
NP-hard:
A problem is NP-hard if it as least as hard as the hardest problems known to be NP. This leads to two possibilities: either the problem is in NP and also considered NP-hard, or it is more difficult than any NP problem.
NP-complete:
This classification is the intersection of NP and NP-hard. If a problem is in NP and also NP-hard, then it is considered NP-complete. This class of problems is arguably the most interesting for its consequences on many other types of problems.
This image from Wikipedia: NP-Hard shows the relation between P, NP, NP-Hard, and NP-Complete.
Minesweeper Problem:
Many people are familiar with the seemingly simple computer game Minesweeper, in which the player clicks locations on the board to reveal numbers, and the numbers correspond to the number of adjacent squares (including corners) that contain mines. Once the player has clicked every square that does not contain a mine, the player wins. If the player clicks a square with a mine, the player loses. From this concept, an NP-complete problem arises. If a picture of a game in progress is given, determine whether or not a gameboard could be generated to fit the scenario shown.
The first picture below shows a game in progress, with 4 mines correctly flagged, many squares correctly labelled, and many squares yet uncovered.



Because I actually played this game (and won), I know that it a solution to the problem did exist. And for a board of this size, it would be relatively simple to find out. But for an m-by-n board, it would not be so simple a question. In order to determine if a solution exists, one must either
1.
Check all possible mine arrangements and check to see if the board picture given fits correctly, or
2.
Correctly guess for each square whether or not there is a mine, eventually filling in the entire board.
Because the second strategy above is valid (if one could correctly guess on every square), the problem is considered NP, and the question could be answered in linear time with the number of squared yet uncovered. However, a deterministic machine could only guess correctly every time in the best case, and the hardness of problems is determined by the worst case.
The second a third pictures illustrate the solution to the game, proving that in this case, the board shown in the first picture was actually valid.
History
To show how difficult this problem is to solve, check out this list of attempted proofs to the problem: History of P=NP Proofs
Evaluation of the permanent begins with Binet and Cauchy in 1812. Despite many attempts, an efficient algorithm for general matrices has proved elusive. After that, a notable breakthrough happened about 40 years ago with the publication of Kasteleyn’s algorithm for counting perfect matching in planar graphs by using O(n3) arithmetic operations in 1961. Then in 1979 Valiant proved that exact computation of the permanent is P-complete, and hence not possible in polynomial time. Since then the focus has shifted to efficient approximation algorithms with precise performance guarantees.
As shown in the graph below, linear programming problems were part of NP and invented by American mathematician George Dantzig in 1947. Linear programming is a method to achieve the best outcome and grows exponentially with the size of the input. However, a polynomial time algorithm with computational steps grows as a power of the number of variables, rather than exponentially was discovered by Russian mathematician Leonid Khachian in 1979. Therefore, he proved that linear programming problems are actually P. Then in 1971 American computer scientist Stephen Cook proved that the satisfy problem is NP-complete, which was the first problem shown to be NP-complete. These discoveries also opened the way to showing other problems are NP-complete problems. In 2000 American mathematician Stephen Smale devised the P vs NP problem.
A theoretical computer mathematician makes THE breakthrough. At first he is overjoyed at his success.
He tests it on the factorization problem and he breaks apart a billion sized number into its factors in mere minutes that would have taken centuries of supercomputer power to solve.
After the excitement wears off, the stark reality of what he now has sinks in.
In his hands lies the key to most of data encryption, the solution to many of scientific problems, optimization of routes such as for market strategies and lest we forget, a $1,000,000 prize from Clay Institute.
Like any human, curiosity gets the best of him and he wanted to test out the full power of his solution. He goes to Wallstreet and in the middle of the a major trade, he easily hacks right through the RSA encryption security and transfers some of the money to a bank account in Switzerland he previously just set up.
He instantly regrets his action, fearing legal reprecutions but none come. Plagued with guilt, he makes good of his stolen money and opens a scientific oriented company to solve major problems in biochemistry, physics, and economics.
- Biochemistry: Protein and enzyme folding for cures
- Physics: the many body problem and chaotic systems
- Economics: Ideal routes to save on time and gas
Check-Out the Travelling Salesman 2012 Movie Info: http://www.imdb.com/title/tt1801123/
Authors:
Jason Kohl (kohl@purdue.edu)
Cameron Young (young149@purdue.edu)
Patrick Kelley (kelley28@purdue.edu)
Intae Whoang (iwhoang@purdue.edu)
Qingshi Zhou(zhou133@purdue.edu)