Contents
[hide]Introduction
The Internet is a huge part of our daily lives. We search for and consume a lot of the information through search engines. One might wonder how search engines work.
In the early 90s, the first search engines used a text-based ranking system to decide the relevance of websites given a query. The way this worked was the pages with the highest occurrences of key words corresponding to the query were determined as relevant. However, an obvious problem with this approach is that suppose one wanted to find information about Purdue. If the query was “Purdue”, one might expect “www.purdue.edu” to be the most relevant site for the query. But if there was a website that used the word “Purdue” more than this site, that would be determined as the most relevant one instead. This is undesirable.
The usefulness of a search engine depends on the relevance of its search results. One would want results to have relevant, popular, and authoritative websites. Modern search engines have more sophisticated methods of determining the relevance of websites based on a search query.
One of the most known and influential algorithms for this is the PageRank algorithm, which we will be exploring in this project. This algorithm was initially developed by Larry Page and Sergey Brin (co-founders of Google) in 1996 as a research project. It was developed based on the idea that different web pages could be ordered in a hierarchy based on its popularity and its relevance.
PageRank Algorithm
Let us understand the Page Rank Algorithm through an example. We use a simplified version of it, which only considers connected graphs. In real life, we could have disjoint sets of websites. Our focus of the algorithm is its linear algebra perspective.
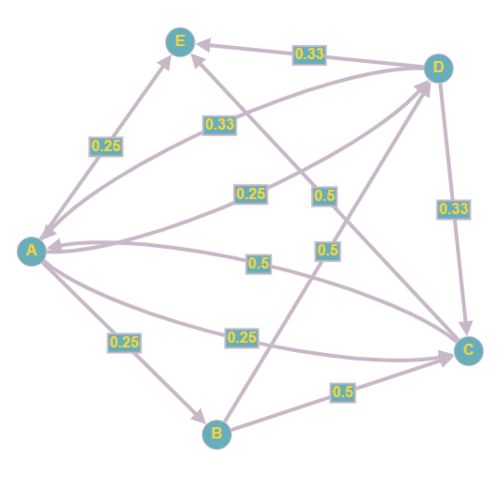
Suppose we have a smaller version of the internet of websites A, B, C, D, E as described in the table below.
| Website | Links to Website(s) | |||||||
|---|---|---|---|---|---|---|---|---|
| A | B, C, D, E | |||||||
| B | C, D | |||||||
| C | A, E | |||||||
| D | A, C, E | |||||||
| E |
We can visualize the relationship of websites by a directed graph with the websites as nodes, edges from vertex u to vertex v if website u references website v, and the weights of edges being the “importance” of website u being transferred to website v equally amongst all its links.
For example, as we can see in the graph, since website A has links to all other pages, it has outgoing edges to all other vertices each with weight $ \frac{1}{4} $ (= 0.25).
Step 1: Create a transition matrix.
Create a transition matrix of the graph with entry (i,j) being the importance that website j transfers to website i. The transition matrix A for this graph would be as follows:
$ \begin{bmatrix} 0 & 0 & \frac{1}{2} & \frac{1}{3} & \frac{1}{4} \\ \frac{1}{4} & 0 & 0 & 0 & \frac{1}{4} \\ \frac{1}{4} & \frac{1}{2} & 0 & \frac{1}{3} & \frac{1}{4} \\ \frac{1}{4} & \frac{1}{2} & 0 & 0 & \frac{1}{4} \\ \frac{1}{4} & 0 & \frac{1}{2} & \frac{1}{3} & 0 \end{bmatrix} $
If there is a website that does not have any outgoing edges, then we distribute its importance to each other website equally. This avoids problems where the resulting PageRank vector becomes 0 in the next step due to calculations.
Step 2: Calculate the PageRank vector.
There are two ways to do this:
Way 1: Iterative version
The PageRank algorithm is an iterative algorithm as described in the official published paper.
Start with an initial n x 1 rank vector v with all entries equal to $ \frac{1}{n} $, where n is the number of websites. Each incoming link should increase the importance of a website, so we update its rank by adding the importance of the incoming links to it. This is the same as multiplying matrix A with v.
This is because in matrix multiplication of a matrix with a vector, we essentially take a dot product of each row to the vector. In the context of this problem, for example, we would be multiplying the importance each website gives to website A in row 1 to its rank, which is each corresponding entry in the vector.
Update the rank vector by repeatedly multiplying matrix A to the new rank vector after each step until it converges. Essentially, we are multiplying A by v in iteration 1, A by Av in iteration 2, …, A by $ A^{(n-1)}v $ in iteration n, until the rank vector converges. This converged rank vector is called the PageRank vector.
$ v_{initial} = \begin{bmatrix} 0.2 \\ 0.2 \\ 0.2 \\ 0.2 \\ 0.2 \end{bmatrix} $
Iteration 1:
$ \begin{bmatrix} 0.21666... \\ 0.1 \\ 0.26666... \\ 0.2 \\ 0.21666... \end{bmatrix} $
Iteration 2:
$ \begin{bmatrix} 0.25416... \\ 0.10833... \\ 0.225 \\ 0.15833... \\ 0.25416... \end{bmatrix} $
Iteration 3:
$ \begin{bmatrix} 0.22881... \\ 0.12708... \\ 0.23402... \\ 0.18125 \\ 0.22881... \end{bmatrix} $
Iteration 4:
$ \begin{bmatrix} 0.23463... \\ 0.11440... \\ 0.23836... \\ 0.17795... \\ 0.23463... \end{bmatrix} $
Iteration 5:
$ \begin{bmatrix} 0.23716... \\ 0.11731... \\ 0.23383... \\ 0.17452... \\ 0.23716... \end{bmatrix} $
Iteration 6:
$ \begin{bmatrix} 0.23438... \\ 0.11858... \\ 0.23541... \\ 0.17362... \\ 0.23438... \end{bmatrix} $
Iteration 7:
$ \begin{bmatrix} 0.23538... \\ 0.11719... \\ 0.23556... \\ 0.17648... \\ 0.23538... \end{bmatrix} $
Iteration 8:
$ \begin{bmatrix} 0.23545... \\ 0.11769... \\ 0.23511... \\ 0.17628... \\ 0.23545... \end{bmatrix} $
As we can see, after 8 iterations, the thousandth place has converged.
The PageRank vector is:
$ \begin{bmatrix} 0.235 \\ 0.117 \\ 0.235 \\ 0.176 \\ 0.235 \end{bmatrix} $
This is an eigenvector of A with eigenvalue 1. It always works out this way. We will compute this directly in Way 2. Later we will explain why this works.
Way 2: Non-iterative equivalent
Let us call the importance of each of the five websites as $ x_1, …, x_5 $. Then, we get the following system of equations:
$ x_1 = \frac{1}{2} \cdot x_3 + \frac{1}{3} \cdot x_4 + \frac{1}{4} \cdot x_5 \\ x_2 = \frac{1}{4} \cdot x_1 + \frac{1}{4} \cdot x_5 \\ x_3 = \frac{1}{4} \cdot x_1 + \frac{1}{2} \cdot x_2 + \frac{1}{3} \cdot x_4 + \frac{1}{4} \cdot x_5 \\ x_4 = \frac{1}{4} \cdot x_1 + \frac{1}{2} \cdot x_2 + \frac{1}{4} \cdot x_5 \\ x_5 = \frac{1}{4} \cdot x_1 + \frac{1}{2} \cdot x_3 + \frac{1}{3} \cdot x_4 $
Each equation comes from the idea that the importance of a website is the sum of the importance of the incoming links to it.
This system of equations is equivalent to asking for the solution to:
$ \begin{bmatrix} 0 & 0 & \frac{1}{2} & \frac{1}{3} & \frac{1}{4} \\ \frac{1}{4} & 0 & 0 & 0 & \frac{1}{4} \\ \frac{1}{4} & \frac{1}{2} & 0 & \frac{1}{3} & \frac{1}{4} \\ \frac{1}{4} & \frac{1}{2} & 0 & 0 & \frac{1}{4} \\ \frac{1}{4} & 0 & \frac{1}{2} & \frac{1}{3} & 0 \end{bmatrix} \cdot \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \end{bmatrix} = \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \end{bmatrix} $
Clearly, we want to find the eigenvector corresponding to the eigenvalue of 1. Solving for it, we get the following form for the eigenvectors:
$ c \cdot \begin{bmatrix} 1 \\ \frac{1}{2} \\ 1 \\ \frac{3}{4} \\ 1 \end{bmatrix} $
The PageRank vector denotes the relative importance of the websites, so we would want all entries to sum to 1. Eigenvectors are all scalar multiples of each other, so we can normalize it by dividing each entry by $ \frac{17}{4} (= 1 + \frac{1}{2} + 1 + \frac{3}{4} + 1) $. This gives us the PageRank vector:
$ \frac{4}{17} \cdot \begin{bmatrix} 1 \\ \frac{1}{2} \\ 1 \\ \frac{3}{4} \\ 1 \end{bmatrix} = \begin{bmatrix} \frac{4}{17} \\ \frac{2}{17} \\ \frac{4}{17} \\ \frac{3}{17} \\ \frac{4}{17} \end{bmatrix} = \begin{bmatrix} 0.23529... \\ 0.11764... \\ 0.23529... \\ 0.17647... \\ 0.23529... \end{bmatrix} \approx \begin{bmatrix} 0.235 \\ 0.117 \\ 0.235 \\ 0.176 \\ 0.235 \end{bmatrix} $
As we can see, this is the same vector calculated by Way 1.
Now that we have seen the non-iterative equivalent, we can explain why we can always arrive to an eigenvector of eigenvalue 1.
A stochastic matrix is a square matrix in which all entries are non-negative. It is called a right stochastic matrix when all the columns sum to 1. Clearly, the transition matrix A from earlier is a right stochastic matrix. In fact, a transition matrix is another name for a stochastic matrix.
A property of a right stochastic matrix is that it always has an eigenvalue of 1.
Proof:
Let A be a right stochastic matrix:
$ \begin{bmatrix} A_{11} & \cdots & A_{1n} \\ \vdots & \ddots & \vdots \\ A_{n1} & \cdots & A_{nn} \\ \end{bmatrix} $
Then, matrix A - I is (where I is the identity matrix)
$ \begin{bmatrix} A_{11}-1 & \cdots & A_{1n} \\ \vdots & \ddots & \vdots \\ A_{n1} & \cdots & A_{nn}-1 \\ \end{bmatrix} $
Each column must sum to 0 now, since each column has an additional -1 term.
This means
$ (A-I)^T \cdot \begin{bmatrix} 1 \\ 1 \\ 1 \\ 1 \\ 1 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix} = 0 \cdot \begin{bmatrix} 1 \\ 1 \\ 1 \\ 1 \\ 1 \end{bmatrix} $
since each column (which is a row in the transpose) sums to 0.
Clearly, matrix A-I has an eigenvalue of 0. This means that the matrix is singular, i.e. it does not have an inverse, and its rows/columns are not linearly dependent, so there is a non-zero vector v in its null space which is the eigenvector of A-I with eigenvalue 0:
$ (A-I) \cdot v = 0 \cdot v \implies A \cdot v - I \cdot v = 0 \implies A \cdot v = I \cdot v \implies A \cdot v = v \implies A \cdot v = 1 \cdot v $
Therefore, matrix A must always have an eigenvalue of 1 with eigenvector v.
This is the first version of the algorithm described in the paper. Since then, it has gone through many changes which are not available publicly.
Importance
In earlier versions of Chrome, users could see the “rank” of a website they were visiting. Google was more open about their algorithm and promoted it more. However, due to manipulation of SEO, (Search Engine Optimization is the process of improving the quality and quantity of website traffic to a website or a web page from search engines), the quality of this ranking decreased as people could “game” the system to rank some websites higher. In 2009, Google removed all references to PageRank from their PR material, and information about it disappeared from the Google Search Console. Later in 2013, they stopped updating the public version of PageRank. No one outside of Google would be able to view other sites’ PageRank. Over the years, Google stopped publicly updating page rank.
While pagerank isn’t actively used and users can’t see pagerank scores, it is the foundation to Google’s search algorithm. Pagerank is one of the many factors used in their search engine. Because of this, search results are still being influenced by this. SEO is also done around this method. The factors that determine pagerank score are still important for SEO and hence are utilized by websites today. Many websites will utilize linking to other websites to boost their rank on the page ranking algorithm. They will also focus on having many internal links as it boosts page rank. People also strategically place links to increase likelihood of people clicking on it. These factors shape the way the internet is set up as most people want to optimize their page rank score. Some people abuse and manipulate this system (regardless of the fact that page rank isn’t that important) to have good SEO. This impacts users’ experience of surfing the web. Not only does pagerank order websites based on existing characteristics (links included, type and nature of content) it also influences how websites are designed and made.
Ethical Implications
The PageRank algorithm came about as Google’s first ambition was to create a fair search engine for all the internet’s needs which resulted in one of the company’s most famous algorithms that made them a fortune. However, though the algorithm’s aim was to remain unbiased to all websites, PageRank is still an algorithm that does not account for human curation or decision but was only intended to be a measure of popularity and relevance of websites instead which can and did present search results that may contain derogatory, racist, sexist, or homophobic materials. As the PageRank also deems the importance of a page through the amount and quality of links that are tied to that page in order to rank and put them on a specific page of Google, this metric of links can and was easily manipulated by websites in order to climb up the PageRank and gain more popularity. Therefore, the lack of human decision and the manipulable nature of the PageRank algorithm sparked controversy and ethical concerns about its usage.
Although Google no longer solely utilizes PageRank to display the order of search results any longer, it was Google’s main algorithm when the company first started in the 2000s. According to the book Algorithms of Oppression, Sergey Brin and Larry Page, the co-founders of Google, had intended PageRank to be a system that is based on “the objective measure of its citation importance that corresponds well with people’s subjective idea of importance” and had acknowledged the bias that could occur in such an advertising-oriented search engine which led to the model for web indexing pages. Although the web indexing aspect of the algorithm ranks pages “according to their importance by measuring how much they were back-linked or hyperlinked to or from” in order to reduce bias, it does not account for the credibility of the sources that are and will be hyperlinked. Consequently, there have been results for certain terms or events that are inaccurate, biased, or derogatory, displaying Google’s lack of responsibility in presenting information on gender or racial identities, unlike more scholarly databases. Therefore, this represents itself in the forms of search results such as the clickbaited and manufactured news reports during the 2016 U.S. presidential election that clouded accurate information sources and one of the most notable instances being the anti-semetic results from the term “Jew.”
In the year 2011, Google received backlash from their users due to the search results for the word “Jew” which included a significant amount of anti-semetic and Holocaust-deinial websites and materials. This situation led Google to issue a statement regarding its search process and encouraged users to utilize the terms “Jews” and “Jewish people” rather than the seemingly pejorative term “Jew” since the company claims that they could do nothing against the usage of the word by White supremacist groups. However, Google states that they do not remove pages if they are unpopular or if they receive complaints but will only remove pages if it violates their guidelines, are required to do so by law, or at the request of the webmaster responsible for the page. Furthermore, though the Anti-Defamation League (ADL), on this matter, declared that Google was not in the wrong for their search results on the term “Jew” because although problematic, the results were computer generated and therefore was not the company’s fault, without the limitations on such derogatory, racist, sexist, or homophobic materials, the PageRank algorithm would remain to have the capability of returning biased and/or unethical search results to certain terms or topics.
Additionally, since the value and importance of a website was no longer determined by the quality of the content but instead, the quotations or hyperlink that it is the subject of in other pages, this metric is important to numerous websites as users do not tend to look past the first page of Google which would decrease the visibility and discoverability of websites and/or company's digital portfolios footsteps. With an additional concept called “search engine optimization,” also known as SEO, which is a set of practices that allows companies and individuals to drive or improve their positioning on Google through organic means. Thus, as SEO drives websites up PageRank through organic search results, this is different than Google’s paid search in which companies pay Google to place its ads first when specific terms are searched. Since numerous websites utilize clicks as profits, SEO became the new scale of measured importance which led websites to utilize a strategy called Google bombing or Google washing by manipulating the algorithm through excessively injecting hyperlinks in to their their websites in order to boost their website’s rank on Google. Google bombing often utilize excessive useless links lead to giving an unfair and unethical advantage to sites that utilize this method of manipulation on the algorithm by ranking them higher on Google than websites that are more relevant or more important. An example of this strategy being utilized is the situation involving Senator Rick Santorum, Republican of Pennsylvania in 2003 who experienced a Google bomb where Dan Savage, gay rights activist and prankster columnist, was connecting Santorum’s name and websites to insults, more specifically, redefining the meaning of the word “Santorum” from his last name to a graphic sexual term which drove foul content relating to the new meaning the top of Google and Page Rank. Additionally other victims that have fallen prey to this manipulative tactic of being associated with insulting phrases include pop singer Justin Bieber and former president George W. Bush.
In another example, Roman Godzich, the SVP of an online retailer of fitness equipment called Smooth Fitness, observed one of his competitors achieve a sudden “organic position” on Google Search where there were “60,000 inbound links from irrelevant websites” added to the competitor’s website which boosted them higher in importance and relevance, according to the PageRank algorithm. Thus, he does not believe that the algorithm is democratically based due to the overpopulation of websites and the easily manipulated algorithm.
Although the PageRank algorithm is one of the most well known algorithms for displaying search results on the internet and being the crown jewel of Google Search, there exists aspects of the algorithm that can lead to derogatory, racist, homophobic, or sexist results in certain situations while allowing users and websites to easily manipulate the algorithm to their advantage as well, raising ethical concerns regarding Google as a company and PageRank as an algorithm.
References
Bénicourt, Arnaud. “PageRank, Parcoursup and Other Moral Machines.” Puissance & Raison, 27 Sept. 2020, www.puissanceetraison.com/en/pagerank-parcoursup-and-other-moral-machines.
Carey-Libbrecht, Liz. “Réseaux.” Inside the Mind of PageRank, translated by Dominique Cardon, vol. 177, La Découverte, 2013, www.cairn-int.info/article-E_RES_177_0063--inside-the-mind-of-pagerank.htm?contenu=auteurs.
Google’s PageRank Controversy : Networks Course Blog for INFO 2040/CS 2850/Econ 2040/SOC 2090. 22 Oct. 2018, blogs.cornell.edu/info2040/2018/10/22/googles-pagerank-controversy.
Holoubek, Sara. “Google’s Update to PageRank Sparks Controversy.” DMNews, 21 Dec. 2007, www.dmnews.com/googles-update-to-pagerank-sparks-controversy.
Noble, Safiya Umoja. Algorithms of Oppression: How Search Engines Reinforce Racism. Illustrated, NYU Press, 2018.
Page, L., Brin, S., Motwani, R., & Winograd, T. (1999). The PageRank citation ranking: Bringing order to the web. Stanford InfoLab.
Raluca Tanase, R. R. (n.d.). Lecture #3. PageRank Algorithm - The Mathematics of Google Search. Retrieved November 30, 2022, from www.pi.math.cornell.edu/~mec/Winter2009/RalucaRemus/Lecture3/lecture3.html.
Rogers, I. (n.d.). The google pagerank algorithm and how it works. Pagerank Explained Correctly with Examples. Retrieved November 30, 2022, from www.ccs.neu.edu/home/vip/teach/IRcourse/4_webgraph/notes/Pagerank%20Explained%20Correctly%20with%20Examples.html