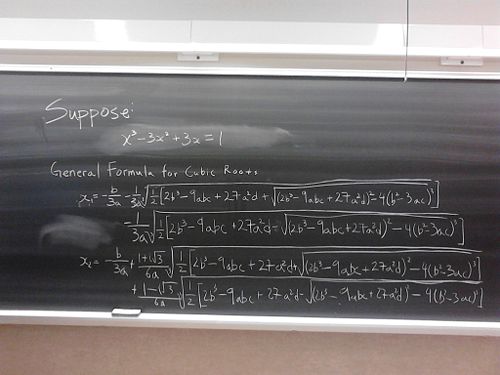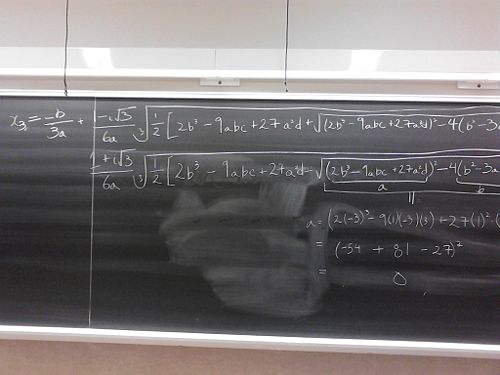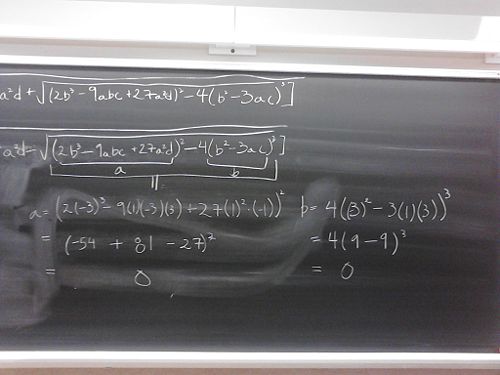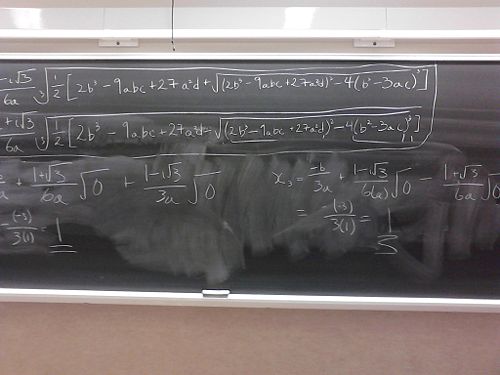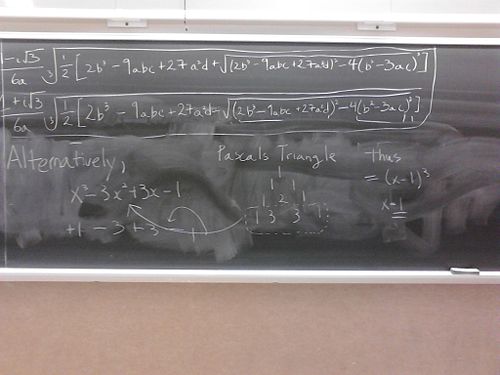On Solving Cubic Functions Equation
One day in my MA 265 lecture (10 Nov.), Professor Uli talked about difficulty in solving polynomial equation of degree n. Specifically, Professor Uli suggested that we do not spend trying to apply the cubic formula for the sake of time, as it will take the entire blackboard to write down the formula.
I decided to see if it really took the entire blackboard to apply the cubic formula. The cubic formula can be found here
Well, no doubt the Professor Uli is right on the amount of writing involved in the using of cubic formula. I intentionally chose a very simple example- selecting less obvious choice of the cubic polynomial would have lengthened the amount of work involved.
One peculiar observation: wikipedia, when presenting the cubic formula, adds a caveat:
"However, this formula is applicable without further explanation only when the operand of the square root is non-negative and a,b,c,d are real coefficients. When this operand is real and non-negative, the square root refers to the principal (positive) square root and the cube roots in the formula are to be interpreted as the real ones."
This restriction, it turns out, is very severe one. If I construct a polynomial with 3 real roots (e.g. x-1, x-2, x-3), the term inside the square root can be negative (-108 for the case above). It is rather strange that the formula will not work for simple roots like 1, 2, and 3.
Back to Daniel's Honor Project