Determinants: an Introduction
I first heard of the concept of determinants of matrices in middle school. It was a scalar number that was produced by a given formula, 'ad - bc'. That definition expanded to include determinants of 3 by 3 matrices, merely another method of producing a scalar number from a matrix. No more was discussed about the determinants. It was neither useful nor significant.
Now, linear algebra has unveiled the original equation of the determinants and where the cookbook recipe of calculating determinants of 2x2 and 3x3 was derived from. Utility of determinants was addressed by showing that the determinant of a matrix can be used to characterize a matrix as singular or nonsingular (and the associated statements) and that to calculate inverse of a that matrix (which is, in turn, useful in solving system of linear equation represented by that matrix). Its geometrical interpretation was discussed briefly in calculating area of a triangle. Properties and proof of them were laid out. Yet of its nature, I have very little appreciation.
Now I would like to believe that there is significance in the concept determinants that I've yet to perceive. It has been emphasized too much for it to be a silly mathematical trick, arbitrary computations of arrangement of number which regurgitates somewhat useful number. For instance, I could accept this explanation of determinants:
"Consider this to furnish you with the "core concept" of what the determinant is. That core concept is very simple to grasp: The determinant is just some number you get out of a particular computation process. It is VERY important that you understand that we are at perfect liberty in maths to define whatever objects we want as long as the definition of it is clear! "
It may be true, but such "liberty" renders the work of mathematics as a serendipitous art. If mathematics is an absolute art, independently complete within the mathematical reality, it would be more satisfying to know that concept of determinants is more than "just some number you get out of a particular computation process."
History may provide a context:
Determinants, and matrices, can be traced back to second century BC in the works of Chinese scholars called the Nine Chapters on the Mathematical Art. It was a collection of practical agricultural and engineering problems, void of rigorous proofs and theorems, but nevertheless incredible mathematical volume that laid a foundation for Asian mathematics (consider that the volume includes mathematical operation similar to Gaussian method, it being introduced in the 19th century. Leibniz considered the word "resultant" when evaluating determinants, Laplace toyed with the concept determinants and solved linear system using determinants alone, and Gauss coined the term determinants as it "determined the properties of the quadratic form", and Cauchy used the determinants in the modern sense, formalizing notion of cofactors and adjoints.
It did not provide a context.
I may need to return to this topic.
-LTY 11 October 2011
++EDIT
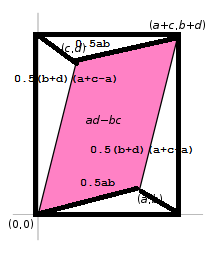
In making connection of determinants with geometry, consider a Cartesian plane with two points, (a,b) and (c,d). Then, determinant is ad - cd. How is this so?
To find the area of the parallelogram, we take the area of the square surrounding the parallelogram and subtract the areas of the triangle inscribed by the square and the parallelogram.
Therefore, the area of the parallelogram is,
= (a+c)(c+d) - 0.5(ab) + 0.5(ab) + 0.5(b+d)(a+c-a) + 0.5(b+d)(a+c-a) = ab + ad + cb + cd - ab - bc - ba = ad - bc
Thus the area of the parallelogram is the the determinants of (a,b) and (c,d):
I am uncertain if this "proof" really is a "proof". That determinants of two cartesian coordinate is the area of the parallelogram produced by the two vectors of the component a,b and c,d; I don't know why that is the case.
However, recall that if the determinant of a matrix is zero, the system of linear equation it represents does not have a unique solution for Ax = 0. Since area of the parallelogram zero only if the two vectors point in the same direction, two vectors are some multiple of the unit vector of that direction. Then, it will be case that there exist values of c1 and c2 not equal to zero that satisfy the equation c1v1 + c2v2 = 0 since, if u represents the unit vector, uc1d1 = uc2d2 = c1d1 = c2d2, where c1, c2, d1, d2 can be any real number. The equation have infinite solutions (with two free variables.. twice the infinity?)
references http://en.wikipedia.org/wiki/Determinant#History
http://forums.randi.org/archive/index.php/t-69414.html
http://www.physicsforums.com/archive/index.php/t-130403.html
http://www.gap-system.org/~history/HistTopics/Matrices_and_determinants.html
Back to Daniel's Honor Project