Notes for Lecture 20, ECE662, Spring 2010, Prof. Boutin
Thursday, April 8th 2010
(Continuation of the linear discriminant of lecture 19)
Let's define the vectors $ \vec{y}_{i} $, $ i \in \left (1,N \right) $ such that $ \vec{y}_{i}\in \mathcal{D} $ and $ \mathcal{D} = \mathcal{D}_{1} \cup \mathcal{D}_{2} $.
Let's define $ \mathcal{D} $ such that $ \mathcal{D} = \mathcal{D}_{1} \cup \mathcal{D}_{2} $.
There exists a vector $ \vec{c} $ for which:
$ \begin{align} \vec{c} \cdot \left ( 1, y_{1}, y_{2}, ... , y_{n} \right ) & > 0, \forall \left ( y_{1}, ... , y_{n} \right ) \in \mathcal{D}_{1} \\ & < 0, \forall \left ( y_{1}, ... , y_{n} \right ) \in \mathcal{D}_{2} \\ \end{align} $
We can transform the second inequality into:
$ \vec{c} \cdot \left ( -1, -y_{1}, -y_{2}, ... , -y_{n} \right ) > 0, \forall \left ( y_{1}, ... , y_{n} \right ) \in \mathcal{D}_{2} $
Example in 1D:
 |
$ g(y_{1}) = -y_{1} + 3.5 $ $ g(y_{1}) = 0 $ is the decision hyperplane. |
$ \vec{c} $ is not unique. It can be any vector with the same direction, it's norm does not count.
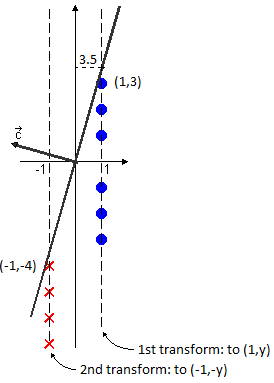
$ \mathcal{D}_{1} \begin{cases} \vec{y} = (3) \\ \vec{y} = (2) \\ \vec{y} = (1) \\ \vec{y} = (-1) \\ \vec{y} = (-2) \\ \vec{y} = (-3) \end{cases} \mathcal{D}_{2} \begin{cases} \vec{y} = (4) \\ \vec{y} = (5) \\ \vec{y} = (6) \\ \vec{y} = (7) \end{cases} g(y_{1}) = cst.y_{1} + cst $
$ \Downarrow $
$ new \mathcal{D}_{1} \begin{cases} \vec{y} = (1,3) \\ \vec{y} = (1,2) \\ \vec{y} = (1,1) \\ \vec{y} = (1,-1) \\ \vec{y} = (1,-2) \\ \vec{y} = (1,-3) \end{cases} new \mathcal{D}_{2} \begin{cases} \vec{y} = (1,4) \\ \vec{y} = (1,5) \\ \vec{y} = (1,6) \\ \vec{y} = (1,7) \end{cases} $
$ \vec{c} \cdot \vec{y} > 0, \vec{y} \in \mathcal{D}_{1} $
$ \vec{c} \cdot \vec{y} < 0, \vec{y} \in \mathcal{D}_{2} $
We modify $ \mathcal{D}_{2} $ such that $ \vec{c} \cdot \vec{y} > 0, \forall \vec{y} \in \mathcal{D} $:
$ new \mathcal{D}_{2} \begin{cases} \vec{y} = (-1,-4) \\ \vec{y} = (-1,-5) \\ \vec{y} = (-1,-6) \\ \vec{y} = (-1,-7) \end{cases} $
$ \vec{c} $ is not unique.
1) Norm ambiguity
If $ \vec{c} $ separates the data, i.e. $ \vec{c} \cdot \vec{y} > 0, \forall \vec{y} \in \mathcal{D} $, then $ \lambda\vec{c} $ also separates it, $ \forall \lambda \in \mathcal{R}_{>0} $.
$ \vec{c} \cdot \vec{y} > 0 \Rightarrow \lambda (\vec{c} \cdot \vec{y}) > 0 $
We can set $ \left | \vec{c} \right | = 1 $.
2) Separation location ambiguity
Here we can take $ \vec{c} = (\beta,-1) $, with any $ \beta \in (3,4) $.
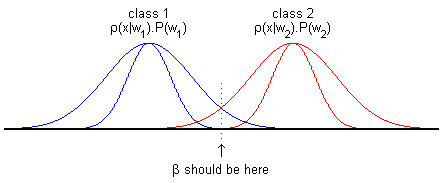
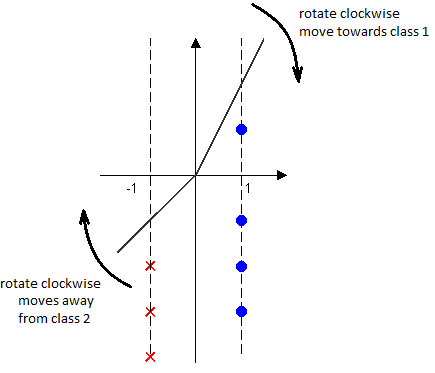
To uniquely define $ \vec{c} $, introduce margin $ b>0 $ and ask that $ \vec{c} $ be the minimum length vector such that $ \vec{c} \cdot \vec{y} \ge b, \forall \vec{y} \in \mathcal{D} $ (after transformation). Then take the separation as $ \vec{c} \cdot \vec{y} = 0 $.
Observe
$ \exists \vec{y}_{i_{0}} \in \mathcal{D} $ such that $ \vec{c} \cdot \vec{y}_{i_{0}} = b $
Otherwise write $ \vec{c} \cdot \vec{y}_{i} = b + \epsilon_{i}, \epsilon_{i} > 0 $
Let $ \vec{c}^\prime = \dfrac{b}{b+\epsilon_{i_{0}}}\vec{c} $ where $ \epsilon_{i_{0}} = min_{i} \epsilon_{i} $
Observe that $ \left | \vec{c}^\prime \right | < \left | \vec{c} \right | $ and $ \vec{c}^\prime \cdot \vec{y} = \dfrac{b}{b+\epsilon_{i_{0}}}\vec{c} \cdot \vec{y} = \dfrac{b}{b+\epsilon_{i_{0}}} ( b + \epsilon_{i} ) \ge b, \forall \epsilon_{i} $ (equality when $ i = i_{0} $)
$ \vec{c} \cdot \vec{y}_{i_{0}} = b $ means $ \vec{y}_{i_{0}} $ belongs to the plane with normal vector $ \vec{c} $ and at distance $ \dfrac{b}{\left | \vec{y}_{i_{0}} \right |} $ from the origin (no other $ \vec{y}_{i} \in \mathcal{D} $ is closer to it).
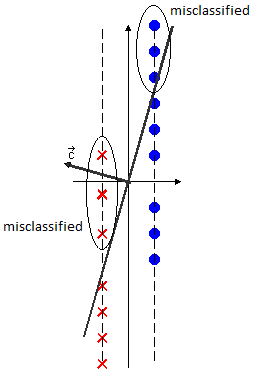
Typically its impossible to satisfy $ \vec{c} \cdot \vec{y} > 0, \forall \vec{y} \in \mathcal{D} $.
Try to do "as best as you can".
Idea:
Try to minimize the number of misclassified training samples.
Let $ J(\vec{c}) = \left | \vec{y}_{1} \in \mathcal{D} \right | \vec{c} \cdot \vec{y}_{1} \le 0 $ be the cost function. Hard to minimize !
Other idea "Perceptron criteria function".
Let $ J_{p}(\vec{c}) = \sum_{\vec{y}_{i} misclassified <br> \vec{y}_{i} \in \mathcal{D}} -\vec{c} \cdot \vec{y}_{i} $
Measures how "far away" you are from classifying all training data correctly.
Geometric interpretation
 |
Distance from yi to plane $ \vec{c} \cdot \vec{y} = 0 $ is: $ \left | projection\, of\, \vec{y}_{i}\, onto\, \dfrac{\vec{c}}{\left | \vec{c} \right |} \right | = \left | \vec{y}_{i} \cdot \dfrac{\vec{c}}{\left | \vec{c} \right |} \right | = \dfrac{}{\left | \vec{c} \right |} . \left | \vec{y}_{i} \cdot \vec{c} \right | $ |
$ (\vec{c} \cdot \vec{y}_{i})\, is\, negative\, when\, \vec{y}_{i}\, is\, misclassified $ |
So $ -\vec{c} \cdot \vec{y}_{i} $ is proportional to the distance from yi to the right side (being right).
Can use gradient descent procedure to minimize $ J_{p}(\vec{c}) $
$ \nabla J_{p}(\vec{c}) = \begin{pmatrix} \dfrac{\partial}{\partial c_{1}} \\ \dfrac{\partial}{\partial c_{2}} \\ \vdots \\ \dfrac{\partial}{\partial c_{n+1}} \end{pmatrix} J_{p}(\vec{c}) = \begin{pmatrix} \dfrac{\partial}{\partial c_{1}} \\ \dfrac{\partial}{\partial c_{2}} \\ \vdots \\ \dfrac{\partial}{\partial c_{n+1}} \end{pmatrix} \sum_{\vec{y}_{i}\, misclassified} -\vec{c} \cdot \vec{y}_{i} = \begin{pmatrix} \sum_{\vec{y}_{i}\, miscl.} -\vec{y}_{i,1} \\ \sum_{\vec{y}_{i}\, miscl.} -\vec{y}_{i,2} \\ \vdots \\ \sum_{\vec{y}_{i}\, miscl.} -\vec{y}_{i,n+1} \end{pmatrix} $
Follow basic gradient descent procedure:
- initialize with guess $ \vec{c}_{1} $
- upgrade to better guess by moving in direction of steepest descent
$ \vec{c}_{2} = \vec{c}_{1} - \underbrace{\eta(1)}_{step\, size} \nabla J_{p}(\vec{c}_{1}) $ - iterate $ \vec{c}_{k+1} = \vec{c}_{k} - \eta(k) \nabla J_{p}(\vec{c}_{k}) $ until convergence
Interpretation:
$ \vec{c}_{k+1} = \vec{c}_{k} - \underbrace{\eta(k) \sum_{\vec{y}_{i}\, misclassified} -\vec{y}_{i}}_{ \begin{matrix} update\, by\, adding\, a\, constant\, \\ multiple\, of\, the\, sum\, of\, all\, \\ misclassified\, samples \end{matrix} } $
When dealing with multiple classes, 2 possible ways:
- take the classes 2 by 2 -> 2(n+1) separations
- or take each class against the rest -> (n+1) separations
(--roy8 17:48, 8 May 2010 (UTC))
