Contents
[hide]Sample Midterm Examination 2
ECE 438
Fall 2016
Instructor: Prof. Mireille Boutin
All questions below are derived from the homework of Prof. Mireille Boutin, all rights reserved by Prof. Mireille Boutin.
135 pts total
(15 pts) 1. List at least three properties of an LTI system.
Solution:
(1)$ e^{j ω_0 n} $ -----> LTI -----> $ {\mathcal H}(ω_0)e^{j ω_0 n} $
where $ {\mathcal H}(\omega) $ is DTFT of unit impulse response h[n]
(2)$ y[n] = x[n] * h[n] $
(3)$ {\mathcal y}(\omega) $=$ {\mathcal X}(\omega) $$ {\mathcal H}(\omega) $
(4)$ Y(z) = X(z)H(z) $
(30 pts) 2. For each ROAC, determine which of these system properties apply. (Just list the letters of the properties that apply.) Below we describe the ROAC of the transfer function of an LTI system.
a) the system is causal;
b) the system is BIBO stable;
c) the system has a well defined and finite frequency response function;
d) the system is an FIR filter;
e) The system is an IIR filter;
f) the unit impulse response of the system is right-sided;
g) the unit impulse response of the system is left-sided;
1.1 ROAC= all finite complex numbers, but not infinity.
1.2 ROAC= all complex numbers, including infinity.
1.3 ROAC= all complex numbers z with |z|>0.5, including infinity.
1.4 ROAC= all finite complex numbers z with |z|>3, but not infinity.
1.5 ROAC= all complex numbers z with |z|<0.5.
1.6 ROAC= all complex numbers z with 2<|z|<3.
Solution:
1.1 ROAC= all finite complex numbers, but not infinity. (b,c,d,f,g)
1.2 ROAC= all complex numbers, including infinity. (a,b,c,d,f,g)
1.3 ROAC= all complex numbers z with |z|>0.5, including infinity. (a,b,c,e,f)
1.4 ROAC= all finite complex numbers z with |z|>3, but not infinity. (e,f)
1.5 ROAC= all complex numbers z with |z|<0.5. (e,g)
1.6 ROAC= all complex numbers z with 2<|z|<3. (e)
Note:
1. The system is causal: |z| > r, including z = infinity.
2. The system is BIBO stable: including unit circle.
3. The system has a well defined and finite frequency response function: same as the system is BIBO stable (including unit circle).
4. The system is an FIR filter: H(z) has no poles in finite complex plane and h[n] is finite duration;
5. The system is an IIR filter: H(z) has poles in finite complex plane and h[n] is infinite duration;
6. The unit impulse response of the system is right-sided: |z| > r (out of unit circle);
7. The unit impulse response of the system is left-sided: |z| < r (in unit circle);
(20 pts) 3. Compute the z-transform of the signal
$ x[n]= 6^{n}u[n] + 8^{n}u[-n+1] \ $
Solution:
$ X(z) = \sum_{n=-\infty}^{\infty} x[n] z^{-n} = \sum_{n=-\infty}^{\infty} (6^{n}u[n]+ 8^{n}u[-n+1]) z^{-n} = \sum_{n=-\infty}^{\infty} 6^{n}u[n] z^{-n} + \sum_{m=-\infty}^{\infty} 8^{m}u[-m+1] z^{-m} $
$ X(z) = \sum_{n=-\infty}^{\infty} (\frac{6}{z})^n u[n] + \sum_{m=-\infty}^{\infty} (\frac{8}{z})^{m}u[-m+1] $
Let k = -m+1, then
$ X(z) = \sum_{n=-\infty}^{\infty} (\frac{6}{z})^n u[n] + \sum_{k=-\infty}^{\infty} (\frac{z}{8})^{k-1}u[k] = \sum_{n=0}^{\infty} (\frac{6}{z})^n + \frac{8}{z} \sum_{k=0}^{\infty} (\frac{z}{8})^{k} $
$ X(z) = \frac{1}{1-\frac{6}{z}} + \frac{8}{z} \frac{1}{1-\frac{z}{8}} = \frac{z}{z-6} + \frac{8}{z} \frac{8}{8-z} , if \quad 6 < |z| < 8 $
$ X(z) = \left\{ \begin{array}{l l} \frac{z}{z-6} + \frac{8}{z} \frac{8}{8-z} &, if \quad 6 < |z| < 8 \\ \text{diverges} &, \quad \text{otherwise} \end{array} \right. $
(20 pts) 4. Compute the inverse z-transform of
$ X(z)=\frac{1}{(1+z)(6-z)}, \text{ ROC } |z|>6 $
Solution:
$ X(z)=\frac{1}{(1+z)(6-z)} =\frac{1}{7} (\frac{1}{1+z} + \frac{1}{6-z}) =\frac{1}{7} (\frac{1}{z} \frac{1}{1+\frac{1}{z}} - \frac{1}{z} \frac{1}{1-\frac{6}{z}}) =\frac{1}{7z} (\frac{1}{1-(-\frac{1}{z})} - \frac{1}{1-\frac{6}{z}}) $
So for $ |z| > 6 $, we have
$ X(z)=\frac{1}{7z} [\sum_{k=0}^{\infty} (-\frac{1}{z})^k - \sum_{k=0}^{\infty} (\frac{6}{z})^k] $
$ X(z)=\frac{1}{7} \sum_{k=-\infty}^{\infty} (-1)^k z^{-k-1} u[k] - \frac{1}{7} \sum_{k=-\infty}^{\infty} 6^k z^{-k-1} u[k] $
Let n = k+1, then
$ X(z)=\frac{1}{7} \sum_{k=-\infty}^{\infty} (-1)^{n-1} u[n-1] z^{-n} + \frac{1}{7} \sum_{k=-\infty}^{\infty} 6^{n-1} u[n-1] z^{-n} $
$ x[n]=[-\frac{1}{7} (-1)^n - \frac{1}{42} 6^n] u[n-1] $
(20 pts) 5. Consider a model of the vocal tract consisting of 2 tubes of equal length l connected to a first tube that is infinitely thin. Assume that l=Tc where c is the speed of sound and T is the period at which you sample the airflow throughout the model. Obtain the transfer function of this model of the vocal tract. (You may use the matrix equations for the tube junction/time delay obtained in class without justification.)
Solution:
$ r_0=\frac{A_1-A_0}{A_1+A_0}=1 $
$ r_1=\frac{A_2-A_1}{A_2+A_1} $
$ r_2=\frac{A_3-A_2}{A_3+A_2}=1 $
$ \left( \begin{array}{c} Ad\left(z \right) \\ Cd\left(z \right) \end{array} \right)= $$ \frac{1}{2}\left( \begin{array} {cc} 1&-1 \\ -1&1 \end{array} \right) z\left( \begin{array} {cc} 1&0 \\ 0&z^{-2} \end{array} \right) \frac{1}{1+r_1} \left( \begin{array}{cc} 1&-r_1 \\ -r_1&1 \end{array} \right) z\left( \begin{array} {cc} 1&0 \\ 0&z^{-2} \end{array} \right) \frac{1}{2}\left( \begin{array} {cc} 1&-1 \\ -1&1 \end{array} \right) \left( \begin{array}{c} Bd\left(z \right) \\ 0 \end{array} \right) $
$ \left( \begin{array}{c} Ad\left(z \right) \\ Cd\left(z \right) \end{array} \right)= \frac{z^{2}}{4\left(1+r_1\right)} \left(\begin{array} {cc} 1+z^{-2}r_1+r_1z^{-2}+z^{-4}&-1-z^{-2}r_1-r_1z^{-2}-z^{-4} \\ -1-z^{-2}r_1-r_1z^{-2}-z^{-4}&1+z^{-2}r_1+r_1z^{-2}+z^{-4} \end{array} \right) \left( \begin{array}{c} Bd\left(z \right) \\ 0 \end{array} \right) $
So $ Ad(z) = \frac{z^{2}}{4\left(1+r_1\right)}(1+z^{-2}r_1+r_1z^{-2}+z^{-4})Bd(z) $
$ H\left( z \right) = \frac{Bd\left( z \right)}{Ad \left( z \right)} = \frac{4z^{-2}\left( 1+r_1 \right)}{1+2r_1z^{-2}+z^{-4}} $
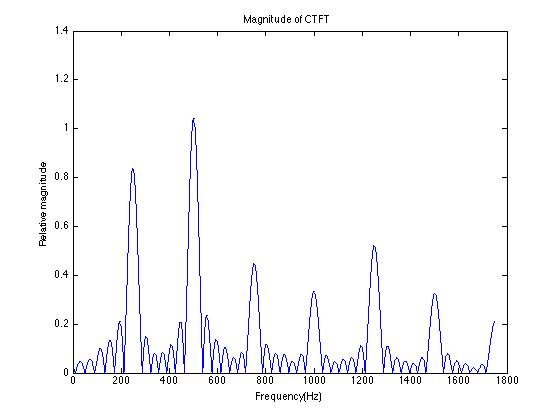
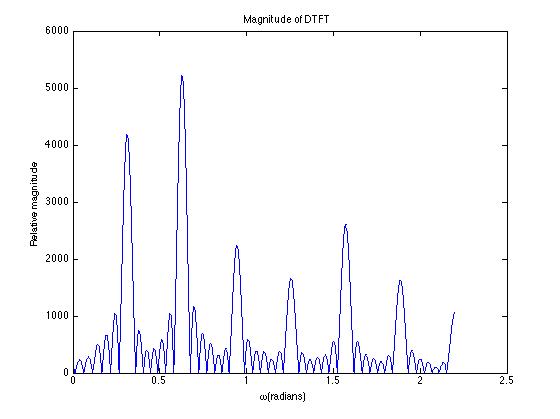
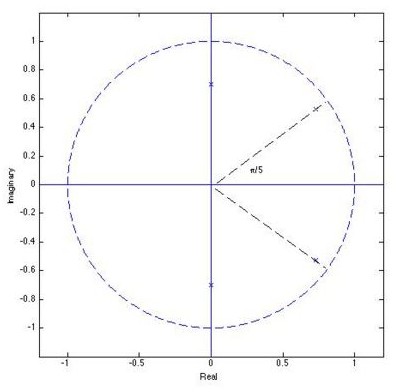
(30 pts) 6. A person is pronouncing a phoneme. The pitch of the person's voice is 250Hz. The phoneme has two formants: a large one at 500 Hz, a weak one at 1.25 kHz. You are given a digital recording of that phoneme. The sampling rate for the recording is 5kHz.
a) From the information given, can you tell the gender of the person?
b) How does the gender of the person influence the location of the local maxima of the magnitude of the frequency response of the vocal tract?
c) Sketch the graph of the magnitude of the CT Fourier transform of the phoneme. How does it compare to the graph of the magnitude of the DT Fourier transform of the digital recording of the phoneme?
d) Sketch the approximate location of the poles of the transfer function H(z) corresponding to the vocal tract of that person when he/she is pronouncing the phoneme.
Solution:
a) pitch period = 1/pitch = 1/250Hz = 4ms.
Males usually have pitch period around 8ms and females have around 4ms. So, it is likely to be female voice.
b) The gender will not influence the location of the local maxima. It only affects the pitch frequency.
c)
d)