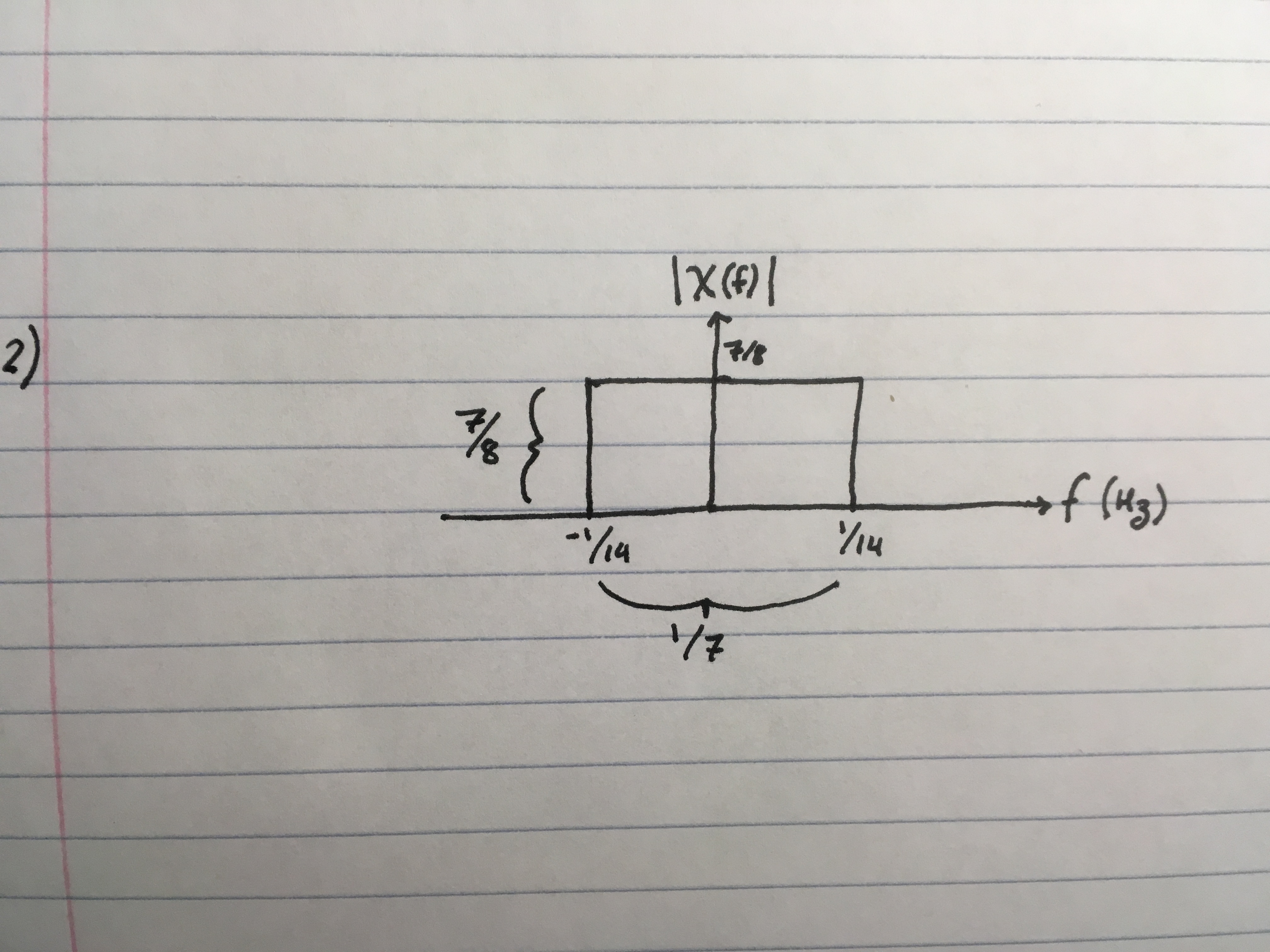Sample Final Exam
ECE 438
Spring 2017
Problems derived and arranged by Aseem Jha.
1. Compute and Sketch the graph of the DTFT of
$ x_d[n] = cos(2 \pi 250 \frac{1}{400} ) $
2. If x(t) is $ \frac{1}{8} sinc(\frac{t-15}{7}) $ find $ \chi(f) $ and plot $ |\chi(f)| $
3. A continuous time signal is such that $ \chi(f) $ is 0 when |f| > 3 KHz. You would like a cutoff at 2KHz and a gain of 5.
a. A sample exists with a sampling rate of 9000 samples/sec. Can you process this signal to make a band limited interpolation? If no, explain why. If yes, explain how.
b. If this sample is downsampled by a factor of 3, can you still make the reconstruction?
4. Find the DFT of $ x[n] = e^{j \frac{\pi}{2} n} * cos( \frac{\pi}{5} n) $
5. Find the N-Point inverse DFT x[n] of $ e^{j \frac{\pi}{3} k} $
6. Compare the total number of operations for a N= 64 point DFT via summation formula, decimation by two, and radix two DFT. Which is the most efficient for N=64? How about for N = 65?
7. Find the Z transform of $ x[n] = 2^{n} * u[n-10] $
8. Find the frequency response in two different ways of $ y[n] + 2y[n-1] + 7y[n-3] = x[n] + 3x[n-2] $ Is this an implicit or an explicit system? What does this tell us about the plot on the Z plane?
9. The sampling rate of a vocal recording is 10KHz. There exists a large formant at 2KHz, medium sized formants at 3 KHz and 1.5 KHz, and a small formant at 4KHz. Below, plot the poles of the frequency response of this vocal recording.
10. Consider a discrete space system defined by $ g[m,n] = h[m,n] ** f[m,n] $ with $ h[m] = \frac{1}{25} * \begin{bmatrix} 1 & 3 & 1 \\ 3 & 9 & 3\\ 1 & 3 & 1 \end{bmatrix} $
What is the response to the following input? (assume 0-boundary condition):
$ \begin{bmatrix} 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 1 & 0 \\ 0 & 1 & 1 & 1 & 0 \\ 0 & 1 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ \end{bmatrix} $
SOLUTION
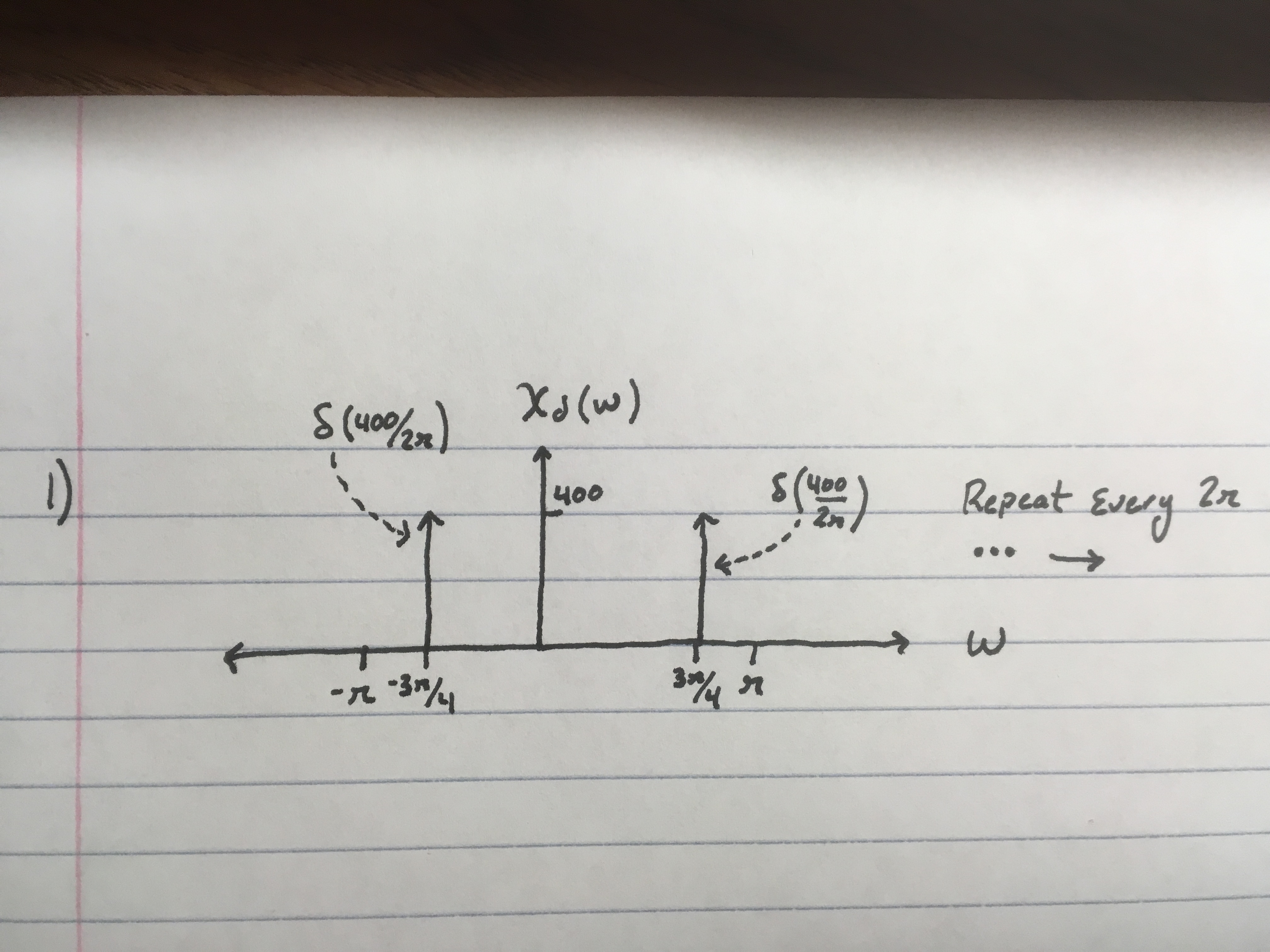
1. $ \chi_d(w) = 400 rep_{2\pi} (\frac{\delta(\frac{400}{2\pi} -250) + \delta(\frac{400}{2\pi} +250)}{2}) $ However, aliasing takes place and the deltas experience a shift to + and - $ 3\pi/4 $ as shown:
NOTE: Images are large, so clicking on them for a preview is advised.
2. By the known relationship between the rect and sinc signals, the $ \chi(f) = \frac {7} {8} rect(7f) e^{-j 17 \pi f} $ The graph is shown below:
NOTE: Images are large, so clicking on them for a preview is advised.
3.
a. Yes! This can be accomplished by passing the signal through a low-pass filter with a gain of 5 and a cutoff at $ \frac {2 \pi 2000} {9000} $
to obtain the desired output.
b. No! The sampling rate is now 3KHz, which is below the Nyquist sampling rate of the highest frequency that may be present (i.e. 3 KHz which would have a Nyquist requirement of a 6 KHz sampling rate at least).
4.
$ x[n] = e^{j \frac{\pi}{2} n} * cos( \frac{\pi}{5} n) $
$ = e^{j \frac{\pi}{2} n} * \frac {1}{2} (e^{j \frac{2 \pi}{10} } + e^{-j \frac{2 \pi}{10} }) $
$ = \frac {1}{2} * e^{j \frac{2 \pi}{4} n} * (e^{j \frac{2 \pi}{10} } + e^{-j \frac{2 \pi}{10} }) $
$ = \frac {1}{2} * e^{j \frac{10 \pi}{20} n} * (e^{j \frac{4 \pi}{20} } + e^{-j \frac{4 \pi}{20} }) $
$ = \frac {1}{2}(e^{j \frac{14 \pi}{20} } + e^{-j \frac{6 \pi}{20} }) $
Compare to the IDFT formula $ x[n] = \sum_{k=0}^{19} (\frac{X_{20}[k]}{20} e^{j \frac{2 \pi}{20} kn}) $
Thus $ X_{20}[k] $ is 10 when k = 6 and 14 and 0 when k = 0,1,2,3,4,5,7,8,9,10,11,12,13,15,16,17,18, and 19.
It is periodic with period 20.
5. $ e^{j \frac{\pi}{3} k} $
$ = e^{j \frac{2\pi}{6} k} $
$ = e^{- j \frac{2\pi}{6} 5k} $
Compare to DFT formula $ X_6[k] = \sum_{k=0}^{5} (x[n] e^{-j \frac{2 \pi}{6} kn}) $
Thus x[n] is 1 when n = 5 and 0 when n = 0,1,2,3,and 4.
It is periodic with period 6.
6. For N = 64:
Summation formula: Complex Ops = $ 2N^{2} - N $ = 8128
Decimation by two: Complex Ops = $ N^{2} + N $ = 4160
Radix two DFT: Complex Ops = $ N log_2(N) $ = 384
The radix two is the most efficient as it has the fewest number of complex operations.
For N = 65:
Summation formula: Complex Ops = $ 2N^{2} - N $ = 8385
Decimation by two: Complex Ops = $ N^{2} + N $ = 4290
For radix 2, assume N = 128 and fill indices 64-125 with zeros.
Radix two DFT: Complex Ops = $ N log_2(N) $ = 896
This is notable because increasing N by one significantly increases the radix two value but it is still far fewer complex operations than the other two.
7.
$ X(z) = \sum_{n=-\infty}^{\infty} (2^{n} u[n-10] z^{-n}) $
$ X(z) = \sum_{k=-\infty}^{\infty} (2^{k+10} u[k] z^{-k-10}) $
$ X(z) =\frac{1024} {z^{10}} \sum_{k=0}^{\infty} ( (\frac {2} {z}) ^{k}) $
$ X(z) =\frac{1024} {z^{10}} \frac{1}{1- \frac {2}{z}} $ for ROC |z| >2
8.
a. Take the Z transform of both sides:
This yields $ Y(z) + 2z^{-1}Y(z) +7z^{-3} Y(z) = X(z) + 3z^{-2}X(z) $
Thus $ \frac {Y(z)} {X(z)} = H(z) = \frac {1 + 3z^{-2}} { 1 + 2z^{-1} + 7z^{-3} } $
Replacing z with $ e^{j \omega} -> H(e^{j \omega}) = \frac {1 + 3e^{-2 j \omega}} { 1 + 2e^{-j \omega} + 7e^{-3 j \omega}} $
b. Take the DTFT of both sides
This yields $ Y(\omega) + 2e^{-j \omega}Y(\omega) +7e^{-3 j \omega} Y(\omega) = X(\omega) + 3e^{-2 j \omega}X(\omega) $
$ =\frac {1 + 3e^{-2 j \omega}} { 1 + 2e^{-j \omega} + 7e^{-3 j \omega}} X(\omega) $
$ = H(\omega) X(\omega) $
Thus $ e^{j \omega} -> H(\omega) = \frac {1 + 3e^{-2 j \omega}} { 1 + 2e^{-j \omega} + 7e^{-3 j \omega}} $
This is an implicit system because it relies on prior values of y. We know from this that there will be poles in the complex plane and that the function will not encompass the whole plane with the possible exceptions of 0 and infinity (as it would if it were explicit). Instead, the polar graph will be either an annulus, a circle, or the outside of a circle, depending on the ROC.
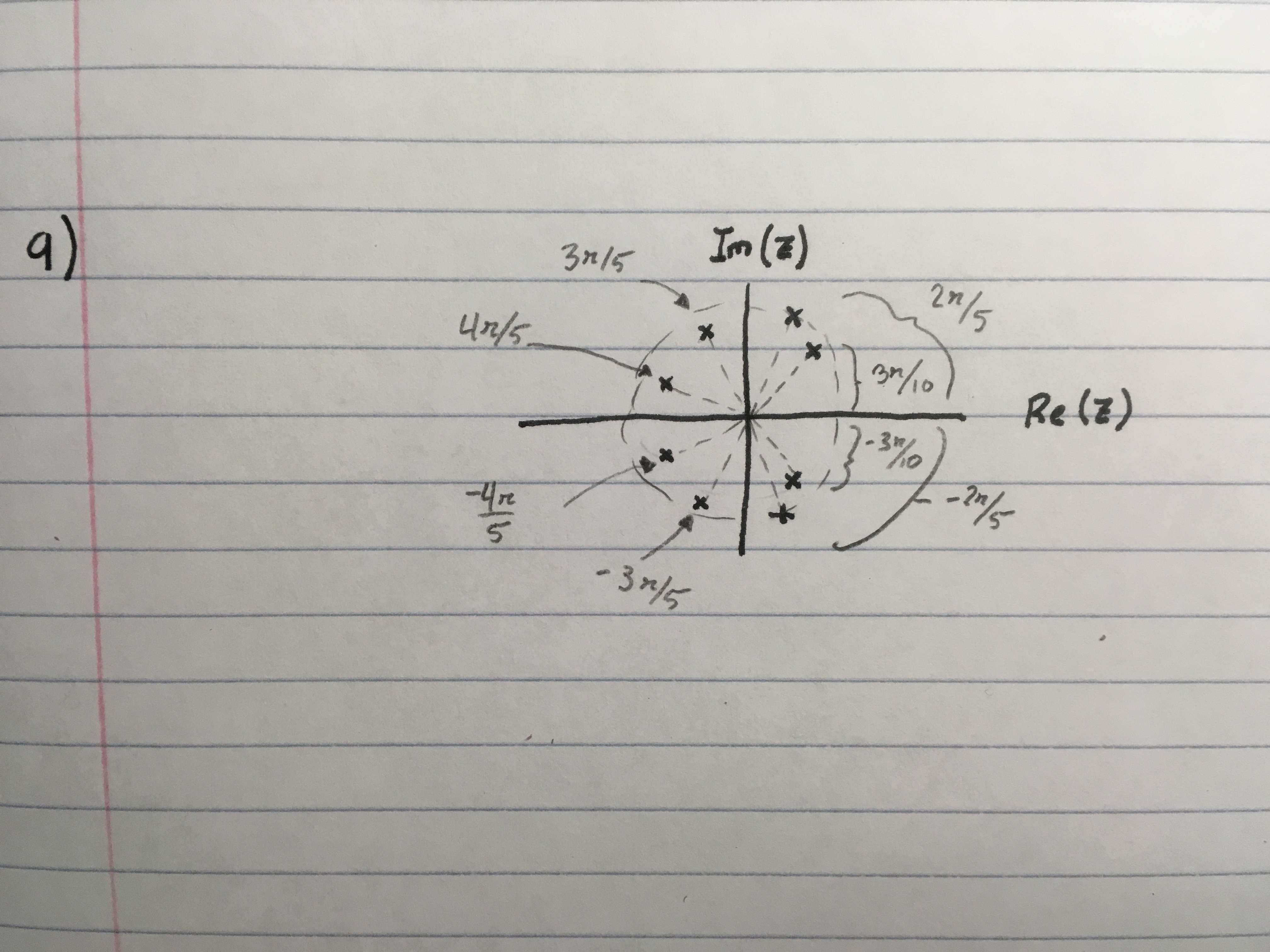
9. Poles at positive and negative $ \frac{2\pi}{5} , \frac{3\pi}{5}, \frac{3\pi}{10}, \frac{4\pi}{5} $
See Figure:
NOTE: Images are large, so clicking on them for a preview is advised.
10. This yields:
$ g[m,n] = \frac{1}{25} * \begin{bmatrix} 1 & 4 & 5 & 4 & 1 \\ 4 & 16 & 20 & 16 & 4 \\ 5 & 20 & 25 & 20 & 5 \\ 4 & 16 & 20 & 16 & 4 \\ 1 & 4 & 5 & 4 & 1 \\ \end{bmatrix} $
Credits
Thanks to Prof. Boutin for inspiring me to make a sample final exam.
Thanks to Hongyu Zhong for providing a template for this sample final with his sample midterm from last semester.
All problems are based on those given by Prof. Boutin in the homework assignments and she maintains all copyright.
NOTE
Last Edited April 24, 2017, 19:20. Minor typos changed for clarity, but was otherwise complete as of midnight April 23.