Of course, Penrose’s tilings did not develop in a vacuum, so it may prove helpful to discuss prior history as well as the work of Penrose. Tilings, or “tessellations” as they are also called, have existed in decoration and design since even before antiquity. The Sumerians, for instance, used clay tiles to decorate their walls and were some of the first to do so. The Romans and other groups which flourished in classical antiquity created decorations with tiles as well. Sumerian and Roman examples can be seen in the two images below, respectively.
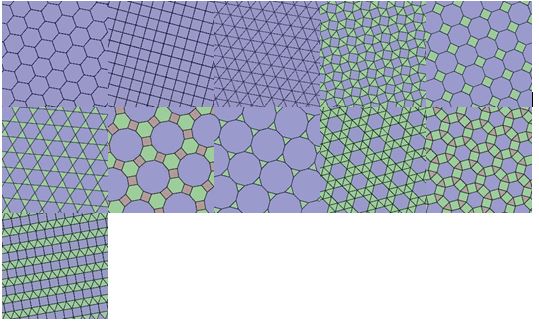
Much later, In 1619, eleven tilings were created by Johannes Kepler using sets of regular polygons in his work Harmonices Mundi. These tilings are called the Archimedean tilings in honor of the Greek mathematician from the 3rd century. All of these tilings can be seen below.
From this point on our discussions of tilings will be more geometric rather than artistic in nature. There is, however, no shortage of aesthetic beauty in the world of tilings, and perhaps no one proves this better than M.C. Escher, who was intrigued by the properties of planes and tilings and made art that was heavily mathematical. More on Escher can be found at this link: http://platonicrealms.com/minitexts/Mathematical-Art-Of-M-C-Escher/
Kepler’s tilings, while not strictly an exercise in mathematics, highlight a curious fact. Periodic tilings must have certain symmetries about them. While they all have translation symmetry, in that one can move the tiling a uniform distance along the direction of the pattern and be left with the same tiling once more, only three-, four-, and six-fold rotational symmetry. In other words, one can only rotate the pattern about the center of a certain point up to three hundred sixty degrees in three, four, or six intervals and be left with the same pattern once more. For example, the tenth tiling above has three-fold symmetry in the center of any triangle, four-fold from the center of any square, and six-fold from any hexagon. Any other type of rotational symmetry would require an aperiodic tiling, as shapes befitting of those symmetries can not fit together in a repetitive way.
During the 1960s, Hao Wang, a philosopher and mathematician, intrigued by aperiodic tilings, asked if there was a collection of tiles which would always result in an aperiodic tiling. Robert Berger found 20,426 such tiles just a few years after Hao Wang posed his question. If one were to use all of these tiles, the tiling would for sure be periodic.
In the 1970s, Roger Penrose drastically lowered this number. He discovered a tiling that was aperiodic and consisted of only six tiles. The picture below is Penrose’s first aperiodic tiling composed of the six tiles. Around the center of the pentagon that is lighter in color, one may notice a five-fold rotational symmetry. This symmetry alone shows that the tiling is aperiodic. Later on, Penrose discovered two aperiodic tilings that were constructed using two types of tiles. One of the tilings consisted of “kites and darts” as tiles and the other tiling consisted of “thick and thin rhombs” as tiles. In the remainder of this work, we will focus on the latter type and delve into the logistics and mathematical logic behind it.
References used in this section:
http://www.ams.org/publicoutreach/feature-column/fcarc-penrose “American Mathematical Society.” AMS, American Mathematical Society, www.ams.org/publicoutreach/feature-column/fcarc-penrose.
“Tessellation.” Wikipedia, Wikimedia Foundation, 18 Nov. 2018, en.wikipedia.org/wiki/Tessellation.