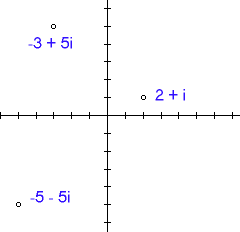Source:[1] Name:Vivek Ravi Subject:Basic Complex number definitions and Concepts
Definition A complex number is one of the form a + bi, where a and b are real numbers. a is called the real part of the complex number, and b is called the imaginary part.
Two complex numbers are equal if and only if their real parts are equal and their imaginary parts are equal. I.e., a+bi = c+di if and only if a = c, and b = d.
Example's for complex numbers are:
2 - 5i.
6 + 4i.
0 + 2i = 2i.
4 + 0i = 4.
The last example above illustrates the fact that every real number is a complex number (with imaginary part 0). Another example: the real number -3.87 is equal to the complex number -3.87 + 0i.
We can visualize complex numbers by associating them with points in the plane. We do this by letting the number a + bi correspond to the point (a,b).
Addition and Subtraction
To add or subtract two complex numbers, you add or subtract the real parts and the imaginary parts.
(a + bi) + (c + di) = (a + c) + (b + d)i. (a + bi) - (c + di) = (a - c) + (b - d)i.
Example.
(3 - 5i) + (6 + 7i) = (3 + 6) + (-5 + 7)i = 9 + 2i.
(3 - 5i) - (6 + 7i) = (3 - 6) + (-5 - 7)i = -3 - 12i.
Multiplication
The formula for multiplying two complex numbers is
(a + bi) * (c + di) = (ac - bd) + (ad + bc)i
Example.
(2 + 3i)(4 + 7i) = 2*4 + 2*7i + 4*3i + 3*7*i2
= 8 + 14i + 12i + 21*(-1) = (8 - 21) + (14 + 12)i = -13 + 26i.