Homework 7, ECE438, Fall 2011, Yimin Xiao's solution for Question 1

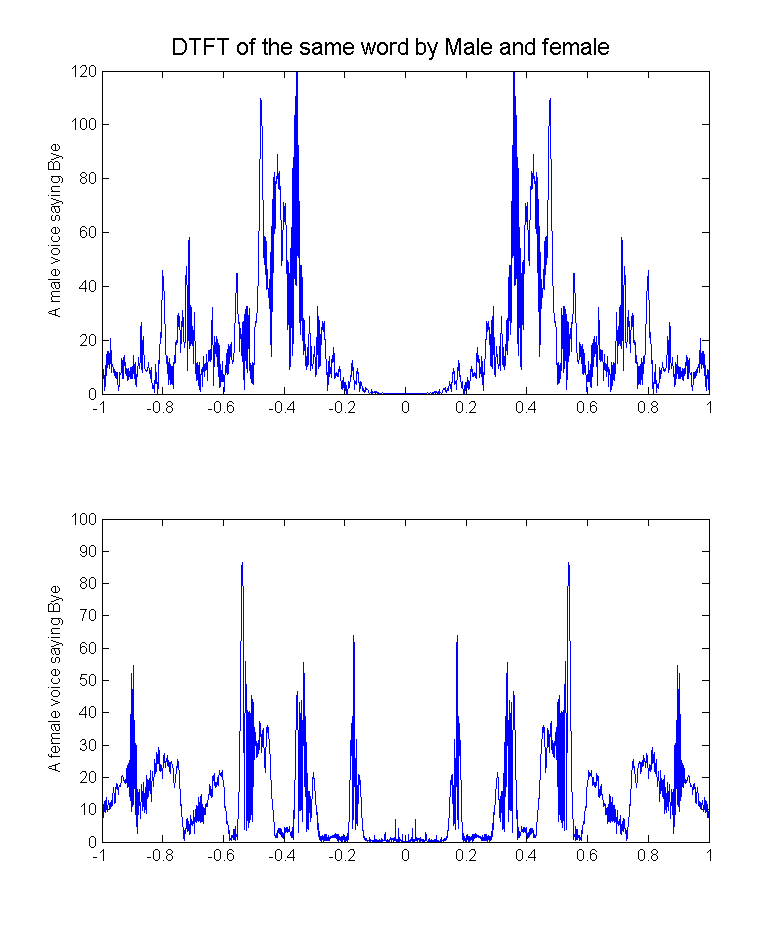
My first idea is that male voice and female voice might have different formants relation, as I plot the DTFT of a same word 'Bye' said by male and female, the plot seems not well behaved and cannot found significant result.

In ECE438 lab9a, the lab manual mentions that the male or female voice distinguishing can be process by looking at the pitch period.

"Typical values for the pitch period are 8 ms for male speakers, and 4 ms for female speakers."

At first I wasn't not convinced by this argument. I believe that voice will not only be different in pitches, but also has formants relations change due to male's vocal folds are different with females, and Adam's Apple makes the sound structurally different on frequency domain.

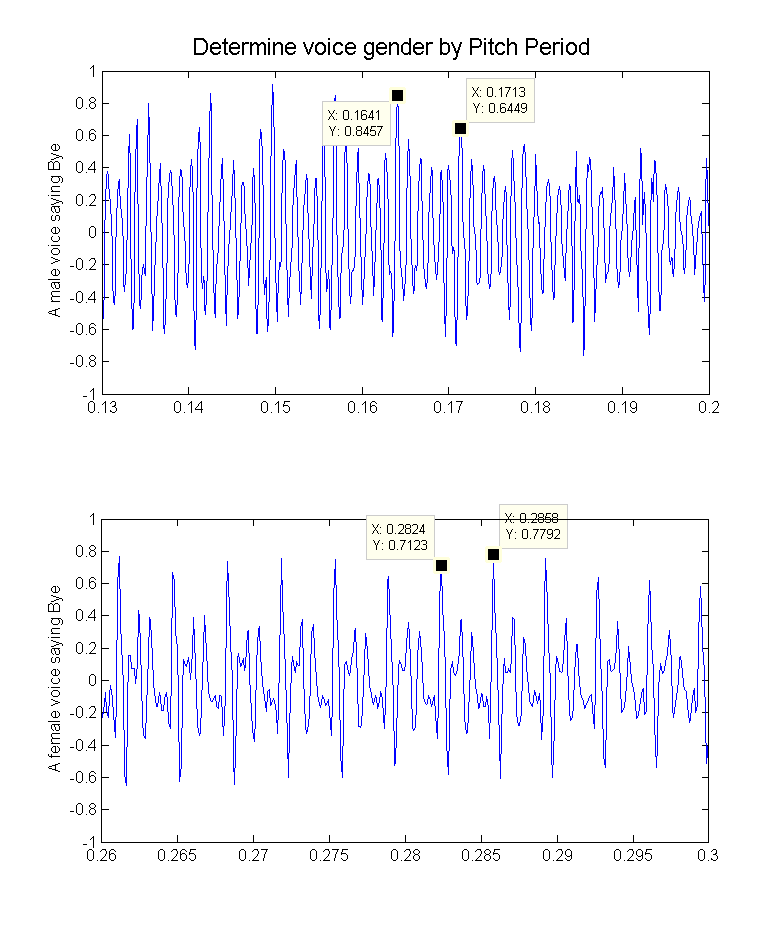
Then I used the same two sound track 'Bye' to test. They match the prediction in lab manual.

Male Pitch Period = 72ms

Female Pitch Period = 34ms

Still not convinced, I tried to modify male voice into female voice and other way around.

And it turns out that the change pitch works for modifying voice into another gender.

Here is a sample from ECE438 Lab9a, a female voice saying five vowels: a e i o u.

Media:ECE438Fall2011HW7_YiminXiao_sound_male_a.wav‎

Here is a modified version, only changed the playing sample rate(slower speed and lower pitch), and sounds like a male voice, a hardly noticeable artificial might present.

Media:ECE438Fall2011HW7_YiminXiao_sound_female_a.wav‎

So, one can conclude that, pitch period can distinguish male voice and female voice with a high accuracy.

Relevant Fun Material:

This video below is a transgender person who teaches on internet how to speak like a female.

I found it amazing that this person can handle these two sounds so well, than at 1:45 the other voice came out I was so surprised.

Caution: In appropriated language appeared in this video.

Question 2

"That's one small step for a man, one giant leap for mankind", was the phrase Purdue alumnus Neil Armstrong planned to say as he stepped foot on the moon during the Apollo 11 mission. However, a careful listening of the recording indicates that the phrase he actually uttered is "That's one small step for man, one giant leap for mankind", skipping the "a" before "man" and thus creating a tautology.

First Approach: (Doesn't work out)

My first concern is the 'a' is missed due to down sampling. Then the following step was taken:

1. zeropad the signal
2. take FFT of the whole zeropadded signal
3. low pass filter the repeated part
4. IFFT back to get the upsampled signal.
   

frustratingly, the signal sounds exactly the same as the original signal.

Then I went back to examinate the original signal(ogg file), then I realize this is a 44100Hz sample file. Which must not be the original data, but had already been upsampled and processed. Since the original data is not accessible and the available data is already the result of the experiment I want to perform, I realized this is not a good approach.

Second approach:(My submission to this problem)

After abandon the first method, I replay the signal again and again, focusing on the two section between "for"s and "man".

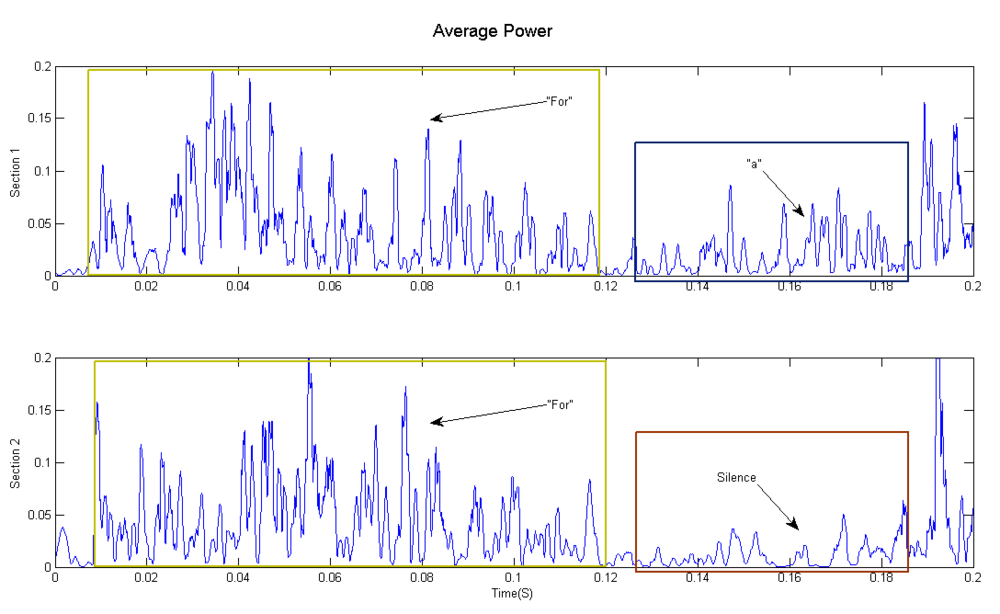
For conveniece in notation, define

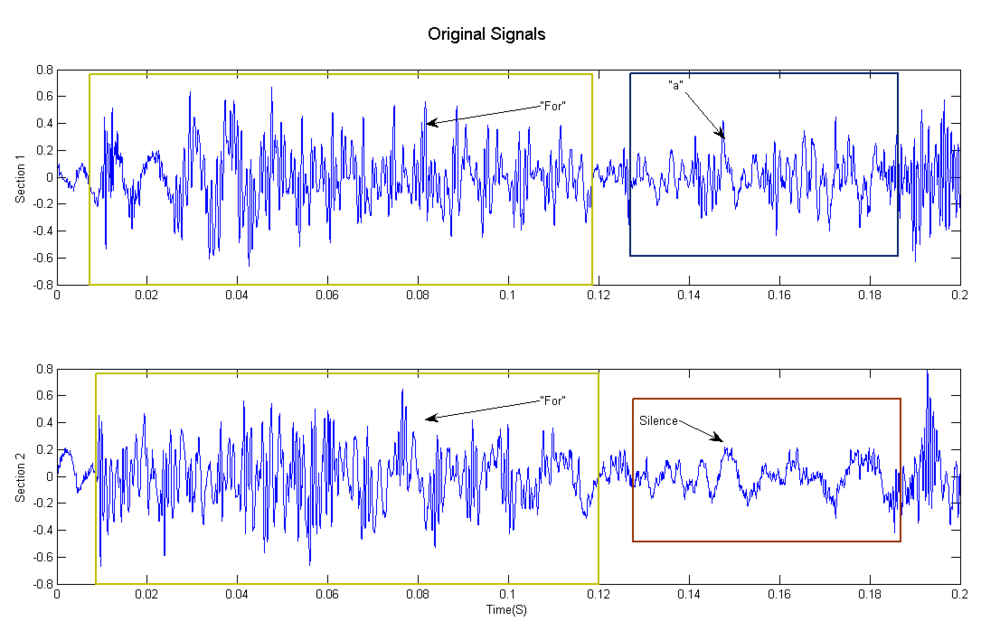
section 1 [for {a?} man]:as the section started at the instant of the first "for" is heard in this record, and end at the instant right before the word "man" is heard.

section 2 [for mankind]: as the section started at the instant of the second"for" is heard in this record, and end at the instant right before the word "mankind" is heard.

I found out that, the first section 1has a slightly higher pitch than section 2.

more precisely, both sections are constructed as two different pitches, from low to high, roughly like a major second scale.

Major second means the "for" sounds like a Do(measured with a tuner as a B note), then "man" sounds like a Re(measured as a C#).

Moreover, the section 2 sounds like two nice equal length notes, two quarter notes, perfect.

But the section 1 sounds like a 1/16 anticipation syncopation(the first note is 3/4 of a quarter note and second is 5/4 quarter note)

This observation strongly suggests that, the "a" was said, and well record. But due to the length of the "a" word, human ear cannot nicely perceive this syllable.

Play the full record again, and the first "For" sounds more like a "fur", but second "For" sounds normal.

But this is only a very subjective musical investigation, cannot support the fact that the "a" exist.

Then following steps were taken:

1. Import section 1 and section 2 in MATLAB.
2. Take DTFT of the two signals.
3. Calculate the average power of the signal with a window size of 10.
4. Plot the signals, DTFTs, Average power and compare the plots.

First look at the original plot. The for parts and a parts are marked out. Section 1 has a stronger oscillation in 'a' part than Section 2's.

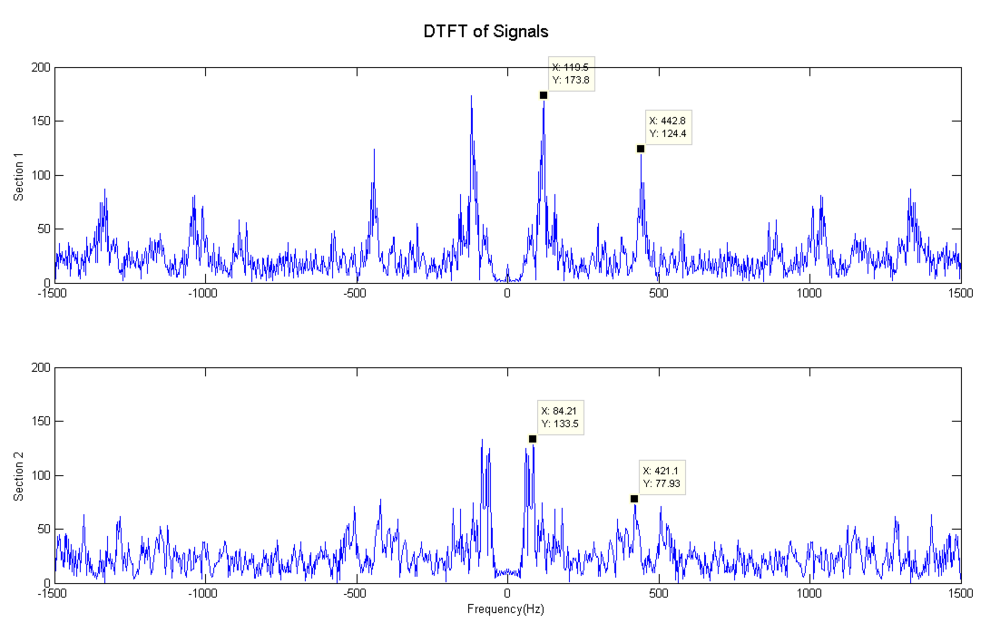
Then inspect the DTFT plot, which do show a frequency difference.

Then finally look at the average power plot, one can conclude that there is a very short syllable in section 1.

But one thing worth mention, the syllable last for about 0.04 seconds, which is probably not perceptible by human ear.

I do not have the data of how long an impulse needs to be for human ear to recognize.

But the shortest echo human ear can distinguish is about 0.1 second. So the assumption of that, a sound lasts about 0.04 s can't be hear clearly by human ear, is reasonable.

Back to Hw7 ECE438F11