Homework 4 Solution, ECE438, Fall 2015, Prof. Boutin
!!!!!!!!!!!!!!!! INSTRUCTOR'S NOTE: THERE IS A MISTAKE BELOW. THE AMPLITUDE OF THE DT FILTER SHOULD NOT BE MULTIPLIED BY 1/TS. -> Corrected!
Question
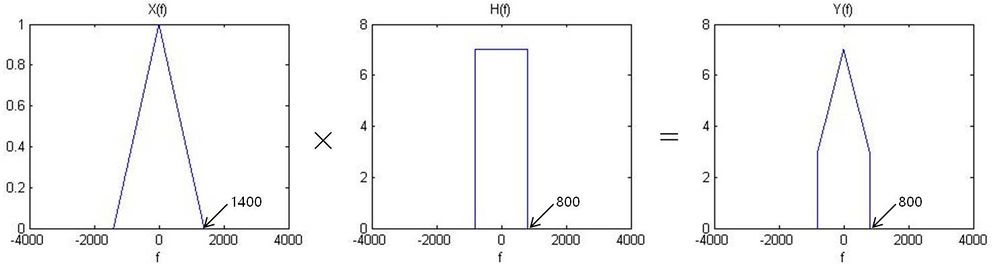
A continuous-time signal x(t) is such that its CTFT X(f) is zero when when |f|>1,400 Hz. You would like to low-pass-filter the signal x(t) with a cut off frequency of 800Hz and a gain of 7. Let's call this desired filtered signal y(t).
- $ x(t) \rightarrow \left[ \begin{array}{ccc} & & \\ & \text{CT filter with frequency response } H(f) & \\ & & \end{array}\right] \rightarrow y(t) $
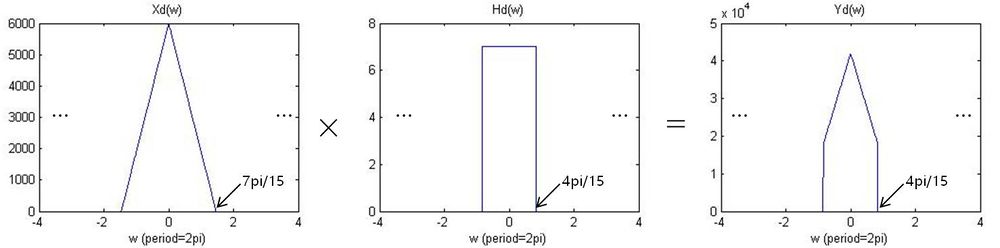
a) Assume that you are only given a sampling of x(t), specifically a sampling obtained by taking 6000 samples per second (samples equally spaced in time). Can one process this sampling in such a way that a band-limited interpolation of the processed (output) DT signal would be the same as y(t)? Answer yes/no. If you answered yes, explain how. If you answered no, explain why not.
- $ x(t) \rightarrow \left[ \begin{array}{ccc} & & \\ & \text{C/D Converter} & \\ & & \end{array}\right] \rightarrow \left[ \begin{array}{ccc} & & \\ & \text{DT filter with frequency response } H_d[\omega] & \\ & & \end{array}\right] \rightarrow \left[ \begin{array}{ccc} & & \\ & \text{D/C Converter} & \\ & & \end{array}\right] \rightarrow y(t) $
- Answer: Yes. Since the sampling frequency is 6000 Hz, there will be no aliasing when we sample a signal which has a maximum frequency of 1400 Hz (fs > 2*fm). The sampled signal Xd(w) has a cutoff frequency $ 7\pi/15 (= 1400*2\pi/6000) $. If we have a discrete-time LPF with a cutoff frequency o$ 4\pi/15 (= 800*2\pi/6000) $, we can have a signal reconstructed same as y(t).
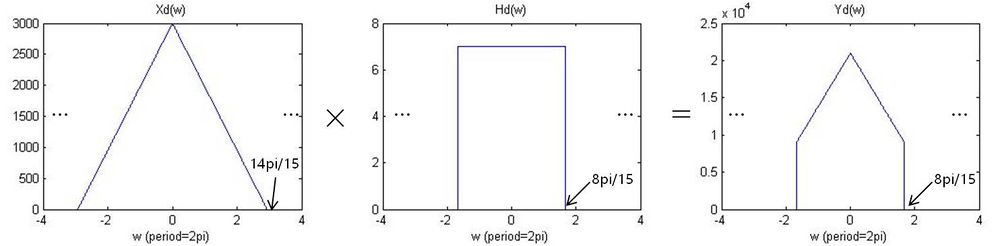
b) Now assume that the sampling from Part a) is downsampled by a factor 2. Can one process this downsampled signal in such a way a band-limited interpolation of the processed (output) DT signal would be the same as y(t)? Answer yes/no. If you answered yes, explain how. If you answered no, explain why not.
- Answer: Yes. Since the sampling frequency is 3000 Hz, there will be no aliasing when we sample a signal which has a maximum frequency of 1400 Hz (fs > 2*fm). The sampled signal Xd(w) has a cutoff frequency $ 14\pi/15 (= 1400*2\pi/3000) $. If we have a discrete-time LPF with a cutoff frequency $ 8\pi/15 (= 800*2\pi/3000) $, we can have a signal reconstructed same as y(t).
Discussion
You may discuss the homework below.
- write comment/question here
- answer will go here