Example of Computation of Fourier series of a CT SIGNAL
A practice problem on "Signals and Systems"
Periodic CT Signal and Its Fourier Coefficients
A Fourier Series of a periodic CT signal is such that:
$ x(t) = \sum_{n=-\infty}^\infty a_k * e^{j*k*w_0*t} $
where
$ a_k = \frac{1}{T} \int_{0}^{T} x(t)* e $($ -j*k*w_0*t $)$ \,\ dt $
If our signal $ x(t) $ consists of only sine and cosine waves, we don't have to do all those complicated integrals in order to find the Fourier coefficients $ a_k $.
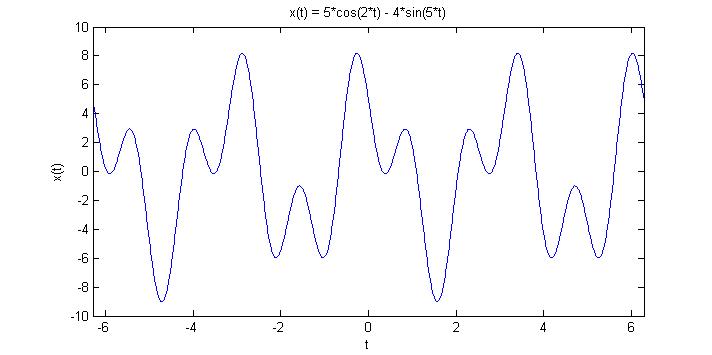
Take the signal $ x(t) = 5cos(2t) - 4sin(5t) $. The graph below proves that it is indeed periodic, with a period $ T = 2\pi $.
$ \,\ sin(x) = \frac{1}{2j} * (e $(jx) $ \,\ - e $(-jx)$ \,\ ) $
and
$ \,\ cos(x) = \frac{1}{2} * (e $(jx) $ \,\ + e $(-jx)$ \,\ ) $
Therefore,
$ x(t) = 5 * \frac{1}{2} * (e $(j2t) $ \,\ + e $(-j2t)$ \,\ ) - 4 * \frac{1}{2j} * (e $(j5t) $ \,\ - e $(-j5t)$ \,\ ) $
$ \,\ x(t) = \frac{5}{2} * e $(j2t) $ \,\ + \frac{5}{2} * e $(-j2t)$ - \frac{4}{2j} * e $(j5t) $ + \frac{4}{2j} * e $(-j5t)
The period $ \,\ T = 2\pi $ so if $ \,\ w_0 = \frac{2\pi}{T} $, then $ \,\ w_0 = 1 $.
Our new equation can now be rewritten as:
$ \,\ x(t) = \frac{5}{2} * e $($ j*w_0*k_1*t $) $ \,\ + \frac{5}{2} * e $($ j*w_0*k_2*t $)$ - \frac{4}{2j} * e $($ j*w_0*k_3*t $) $ + \frac{4}{2j} * e $($ j*w_0*k_4*t $)
where $ k_1,k_2,k_3, $ and $ k_4 $ correspond to { $ \frac{5}{2}, \frac{5}{2} , -2 , \frac{2}{j} $ }, respectively.
Therefore, we can take the coefficients of the equation and the $ k $ values to determine the Fourier coefficients.
$ \mathbf{a_2} = \mathbf{\frac{5}{2}} $
$ \mathbf{a} $-2$ = \mathbf{\frac{5}{2j}} $
$ \mathbf{a_5} = \mathbf{-2} $
$ \mathbf{a} $-5$ = \mathbf{\frac{2}{j}} $
$ a_x = 0 $ elsewhere.