Part A
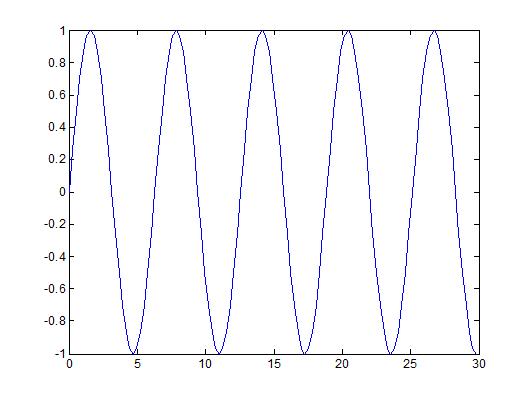
The original signal shown in the first plot is y(t) = sin(t) with a period of $ 2\pi $
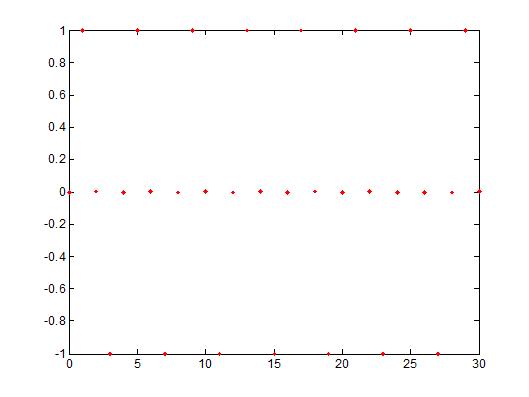
The plot on the left shows the same signal but in DT (y[n] = sin(n)). The sampling frequency is at $ \pi/2 $ (y[n] = sin($ (\pi/2) $*n)). The signal repeats itself every 4 sec so that y[n] = y[n+4]. No = k * $ \frac{2\pi}{\pi/2} $ ==> No = k * 4 so that the signal repeats itself every 4 seconds.
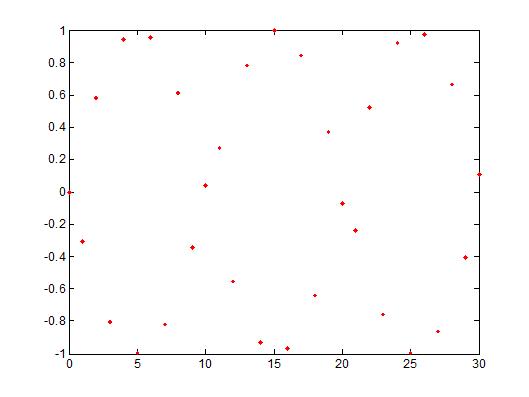
The right picture is taken at a frequency of 10000 Hz so that y[n] = sin(10000 * n). As you can see the signal is not periodic because the value of No is not an integer. $ No = k * \frac{2\pi}{10000} = \frac{\pi}{5000} $ and this is not a rational integer. Therefore the signal in DT is not periodic.
Part B
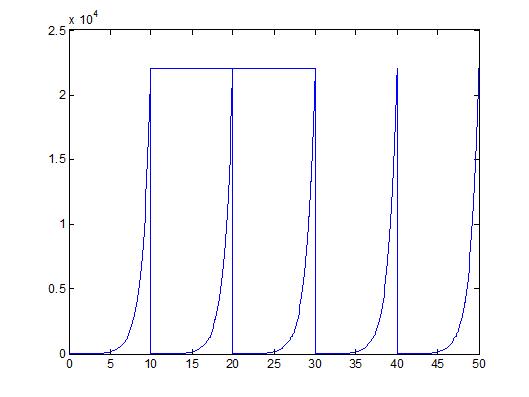
The signal is y(t) = exp(t).
I don't know why there is a line connecting the first two spikes, but just pretend they are not there.
As you can see, this originally non periodic function is not periodic because it repeats itself every 10 seconds.
This means that the fact that y(t) = exp(t - k*T), given that T = 10, is true and therefore the function is periodic now.