Part C: Linearity
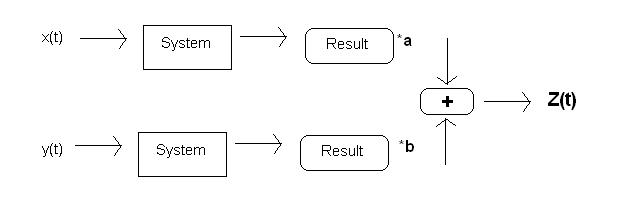
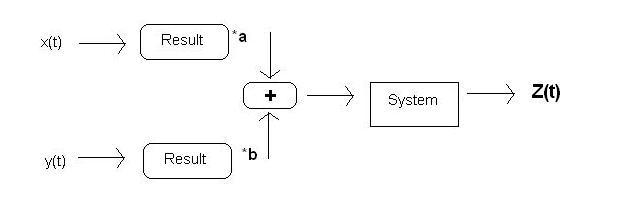
A linear system is a system such that for any constants $ a $ and $ b $ on the complex plane, inputs $ x(t) $ and $ y(t) $ produce the same $ z(t) $ no matter which of the following two paths they take through the system:
Path One:
Path Two:
Example of a Linear System
For this example, we take $ x $1$ (t) = x $ and $ x $2$ (t) = 0 $. We will also take $ a = 1 $ and $ b = 5 $. Taking the "first path" produces a result of $ z $1$ (t) = 1*x^2 +5*0 $, while taking the "second path" produces a result of $ z $$ (t) = (1*x + 0*5)^2 = x^2 $. Because $ z $1$ (t) $ = $ z $2$ (t) $, the system is linear.
Example of a Non-Linear System
For this example, let's take $ x $1$ (t) = x $ and $ x $2$ (t) = 1 $. Again, we'll also take $ a = 1 $ and $ b = 5 $. Taking the "first path" produces a result of $ z $1$ (t) = 1*x^2 +5*1 $, while taking the "second path" produces a result of $ z $$ (t) = (1*x + 1*5)^2 = x^2 + 10*x + 25 $. Because $ z $1$ (t) $ != $ z $2$ (t) $, the system is non-linear.
