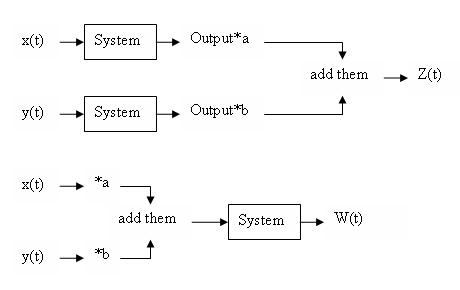
Not words but DIAGRAMS
If W(t)=Z(t) then it is linear
Non-Linear System
take $ \,\ x(t) = 3t^2, y(t) = t^3 $
and $ \,\ a = 2, b = 3 $
The system squares the function that goes in.
Then we get
$ \,\ Z(t) = 2t^4 + 3t^6 $ and
$ \,\ W(t)= (2t^2+3t^3)^2 $
we see that Z(t) and W(t) are not equal so they are not linear.
Linear System
I am taking the same values except now the system just multiplies it by 4.
$ \,\ Z(t) = 8t^2 + 12t^3 $ and
$ \,\ W(t)= 4(2t^2+3t^3) $
and BAM we get a linear function because Z(t)=W(t)