Honors Code: Do not look at the solution until you are done with your homework. Do not edit your homework after you have looked at the solution.
Contents
[hide]Homework 10, ECE438, Fall 2016, Prof. Boutin
Question 1
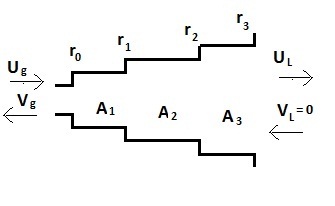
Consider a model of the vocal tract consisting of three tubes of equal length l connected to a first tube that is infinitely thin. Assume that l=Tc where c is the speed of sound and T is the period at which you sample the airflow throughout the model.
a) Obtain the transfer function of this model of the vocal tract. (You may use the matrix equations for the tube junction/time delay obtained in class without justification.)
$ r_0=\frac{A_1-A_0}{A_1+A_0}=1 $
$ r_1=\frac{A_2-A_1}{A_2+A_1} $
$ r_2=\frac{A_3-A_2}{A_3+A_2} $
$ \left( \begin{array}{c} Ad\left(z \right) \\ Cd\left(z \right) \end{array} \right)= $$ \frac{1}{2}\left( \begin{array} {cc} 1&-1 \\ -1&1 \end{array} \right) z\left( \begin{array} {cc} 1&0 \\ 0&z^{-2} \end{array} \right) \frac{1}{1+r_1} \left( \begin{array}{cc} 1&-r_1 \\ -r_1&1 \end{array} \right) z\left( \begin{array} {cc} 1&0 \\ 0&z^{-2} \end{array} \right) \frac{1}{1+r_2} \left( \begin{array}{cc} 1&-r_2 \\ -r_2&1 \end{array} \right) z\left( \begin{array} {cc} 1&0 \\ 0&z^{-2} \end{array} \right) \frac{1}{2}\left( \begin{array} {cc} 1&-1 \\ -1&1 \end{array} \right) \left( \begin{array}{c} Bd\left(z \right) \\ 0 \end{array} \right) $
$ \left( \begin{array}{c} Ad\left(z \right) \\ Cd\left(z \right) \end{array} \right)= \frac{z^{3}}{4\left(1+r_1\right)\left(1+r_2\right)} \left(\begin{array} {cc} X&Y \\ Y&X \end{array} \right) \left( \begin{array}{c} Bd\left(z \right) \\ 0 \end{array} \right) $
where $ X=z^{-2} \left( r_2 (r_1 z^{-2}+1)+r_1 z^{-2}+z^{-4} \right)+r_1 z^{-2}+z^{-2}r_2 (r_1+z^{-2})+1 $
and Y is some polynomial in $ z^{-1} $ (the actual expression is irrelevant). We have
$ H\left( z \right) = \frac{Bd\left( z \right)}{Ad \left( z \right)}=\frac{4 z^{-3} (1+r_1)(1+r_2)}{X} $
Simplifying X, we get
$ H\left( z \right) = \frac{4z^{-3}\left( 1+r_1 \right) \left( 1+r_2 \right)}{z^{-6}+r_1r_2z^{-4}+\left(r_1+r_2 \right)z^{-4} + r_1r_2z^{-2} + \left(r_1+r_2 \right)z^{-2}+1} $
b) How many formants could one create with such a model? Explain.
Answer: 3 formants.
Explanation: The denominator of the transfer function is a polynomial of degree 6 in $ z^{-1} $. Thus, it has 6 roots (i.e. solving the equation polynomial=0 will yield 6 solutions). These 6 roots can be divided into 3 pairs of complex conjugate roots. (More specifically, each of the 3 pairs of roots can be written in the form a+(-)bj, and b can be 0 in the case of a double real root.) Thus, the transfer function has 6 poles: 3 in the upper complex plane, and 3 in the lower complex plane. Each of the 3 poles in the upper complex plane yields a local maximum in the magnitude of the frequency response within the interval $ [0,\pi] $. The other 3 poles create symmetric formants in the interval $ [-\pi,0] $.
c) Explain how one would control the location of the formants with such a model.
The location of the three formants are controlled by the value of the 6 roots. The values of the roots is determined by the coefficients of the polynomial mentioned in part (b). The coefficients are determined by the reflection coefficients $ r_1 $ $ r_2 $. This means that we can control the location of the formants by changing the ratio of the areas of consecutive tubes.
Question 2
Why do the poles of the transfer function of the vocal tract always come in complex conjugate pairs? Explain.
If we write the transfer function H(z) as H(z)=P(z)/Q(z), where P(z) and Q(z) are polynomials, then we see that the poles of the transfer function are the roots (zeros) of the polynomial Q(z). The polynomial Q(z) has real coefficients since the system can be written as a difference equation with real coefficients (because the vocal tract transform real signals into real signals). In general, the roots of a polynomial with real coefficients always come in complex conjugate pair. This is because, if $ z_0 $ is root of a polynomial p(z) with real coefficient, then $ p(z_0)=0 $. Conjugating both sides of the equation we get that $ (p(z_0))*=0*=0 $. But since the polynomial p(x) has real coefficients, $ (p(z_0))*=p(z_0*) $. Thus $ p(z_0*)=0 $ and so the conjugate $ z_0 $ is also a root.
Question 3
We have seen that the transfer function of the vocal tract for voiced phonemes has poles (which create the formants).
a) What does this imply regarding the difference equation representing the system (in discrete-time)?
This implies that the difference equation must have the form
$ \sum_{i=0}^{M} b_i y[n-i] =\sum_{k=1}^{N} a_k x[n-k] $
with M>0. (Note that M is equal to the number of poles in the finite complex plane.)
b) Could the vocal tract be modeled using an FIR filter? Explain.
No, it must be an IIR filter as it must have poles. As explained in (a), the difference equation describing the system involves values of the output y[n] at previous times.
Questions 4
Warning: do not confuse the period of the sampling with the period of the pulse train produced by the vocal tract (1/pitch). Use different variables!
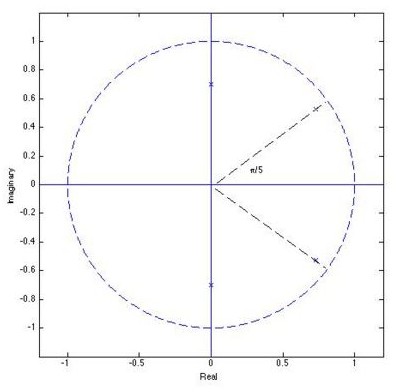
A person is pronouncing a phoneme. The pitch of the person's voice is 250Hz. The phoneme has two formants: a large one at 500 Hz, a weak one at 1.25 kHz.
You are given a digital recording of that phoneme. The sampling rate for the recording is 5kHz.
a) From the information given, can you tell the gender of the person?
pitch period = 1/pitch = 1/250Hz = 4ms.
Males usually have pitch period around 8ms and females have around 4ms.
So, it is likely to be female voice.
b) How does the gender of the person influence the location of the local maxima of the magnitude of the frequency response of the vocal tract?
The gender will not influence the location of the local maxima. It only affects the pitch frequency.
c) Sketch the graph of the magnitude of the CT Fourier transform of the phoneme. (Put three dots "..." in the inaudible region of the spectrum.) How does it compare to the graph of the magnitude of the DT Fourier transform of the digital recording of the phoneme?
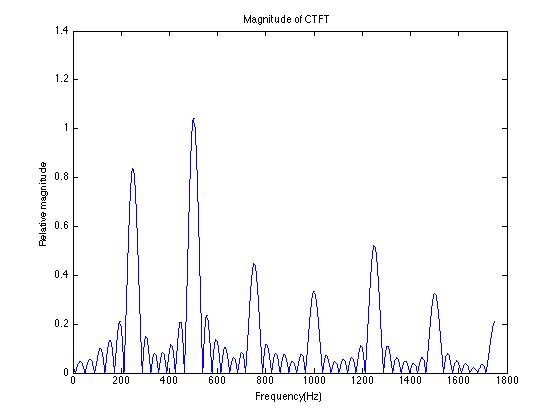
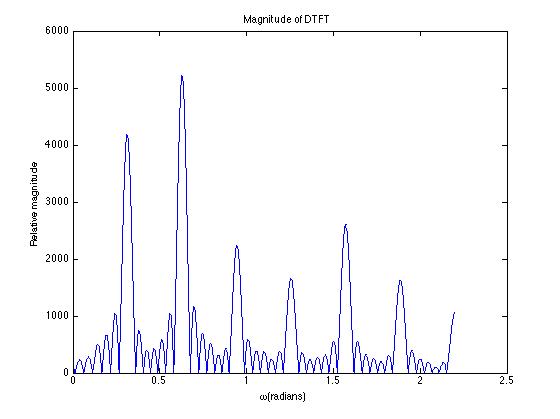 There are three differences: the DTFT of the digital recording looks like the CTFT of the original analog signal, with the amplitude rescaled (multiplied) by a factor $ \frac{1}{T}=5,000 $, the frequency axis rescaled (multiplied) by a factor $ 2\pi T=2\pi\frac{1}{5,000} $, and the whole thing repeated every $ 2\pi $.
There are three differences: the DTFT of the digital recording looks like the CTFT of the original analog signal, with the amplitude rescaled (multiplied) by a factor $ \frac{1}{T}=5,000 $, the frequency axis rescaled (multiplied) by a factor $ 2\pi T=2\pi\frac{1}{5,000} $, and the whole thing repeated every $ 2\pi $.
d) Sketch the approximate location of the poles of the transfer function H(z) corresponding to the vocal tract of that person when he/she is pronouncing the phoneme.