Periodic versus non-periodic functions (hw1, ECE301)

Read the instructor's comments here.

Periodic Functions in Continuous Time

• Functions are classified as periodic if there exists $ T>0\! $ such that $ y(x+T)=y(x)\! $.

The following is an example of a periodic function:

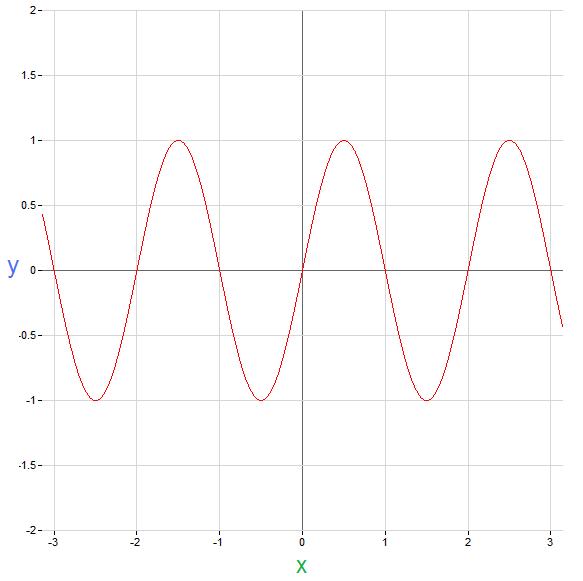
This function is periodic because $ y(x)=y(x+T)\! $ for $ T=2, 4, 6\! $ etc.

Non-Periodic Functions in Continuous Time

• Functions are classified as non-periodic if there exists no $ T>0\! $ such that $ y(x+T)=y(x)\! $.

The following is an example of a non-periodic function:

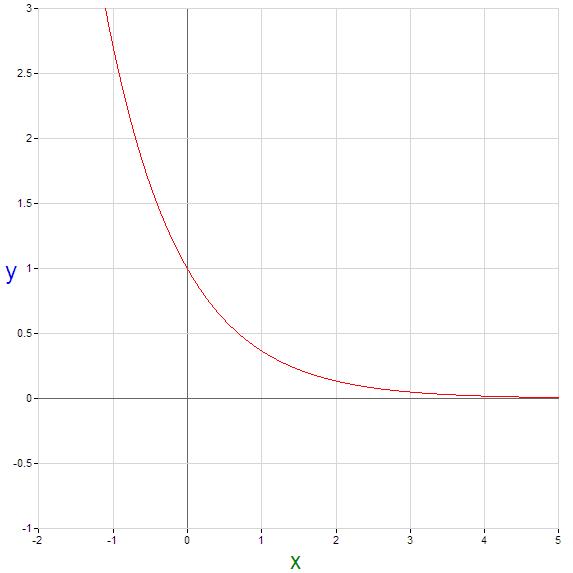
This function is not periodic because there exists no T where $ y(x)=y(x+T)\! $.