Contents
Periodic versus non-periodic functions (hw1, ECE301)
Read the instructor's comments here.
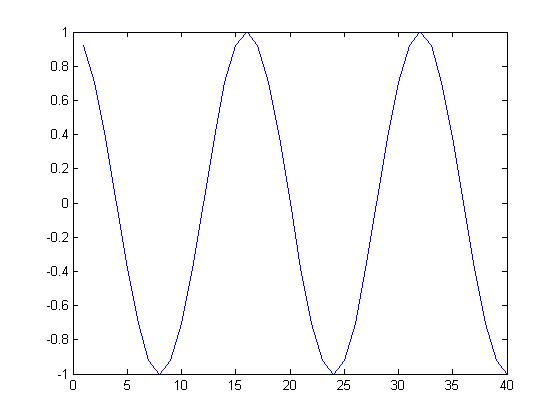
Periodic Functions
A Periodic Function is a function where the entire graph is formed from copies of a particular portion at specified intervals.
The Function :$ f(x) = sin(x)\,\! $ is a periodic function with a Period :$ T = 2*\pi\,\! $.
This sine wave function repeats itself every period of :$ 2*\pi,\! $
Periodic function $ f(x) = sin(x) $. The graph consists of copies of the values $ T = 0 $ to $ T = 2*\pi $.
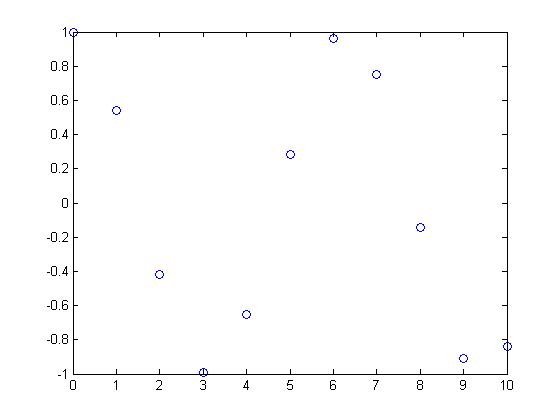
Non-Periodic Functions
The Function :$ f(x) = cos(e^x)\,\! $ is non-periodic since the graph does not consist of copies of one part of the graph positioned one after the other.
Non-Periodic function $ f(x) = cos(e^x) $. The graph has no visible repeated copies of one part of the graph.
