Periodic versus non-periodic functions (hw1, ECE301)
Read the instructor's comments here.
Periodic Functions
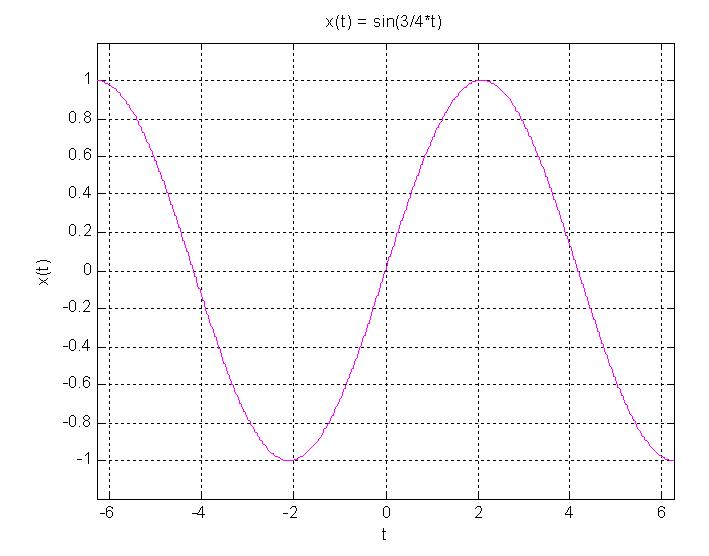
A continuous time signal is periodic if there exists a value $ T $ such that $ x(t + T) = x(t) $.
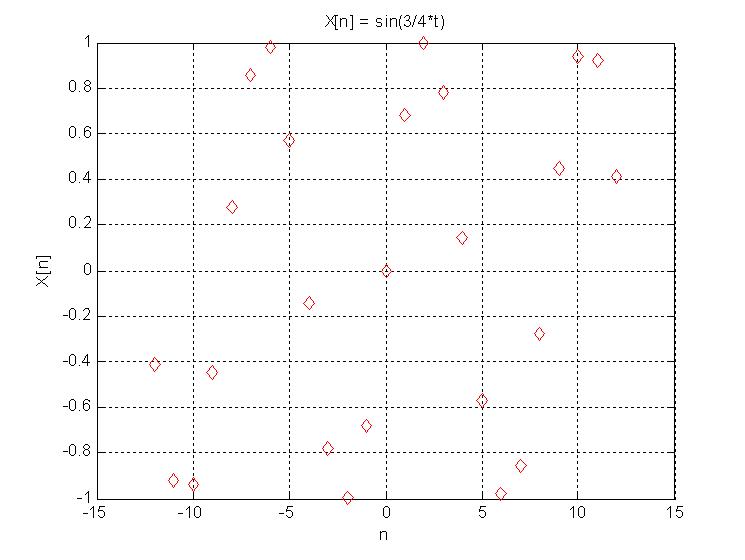
A discrete time signal is periodic if there exists a value $ N $ such that $ X[n + N] = X[n] $.
As you can see in the graph, at time $ t = 0 $, $ x(t) = 0 $. This occurs again at $ t = 4/3\pi $, and again at $ -4/3\pi $.
Non-Periodic Functions
Using the same equation as above in discrete time, $ X[n] = sin(3/4*n) $ does not produce a periodic function.
In the graph below, the function seems to be merely a scattering of points and doesn't follow a periodic pattern (due to the irrationality of $ \pi $).