Periodic Function: Square Wave
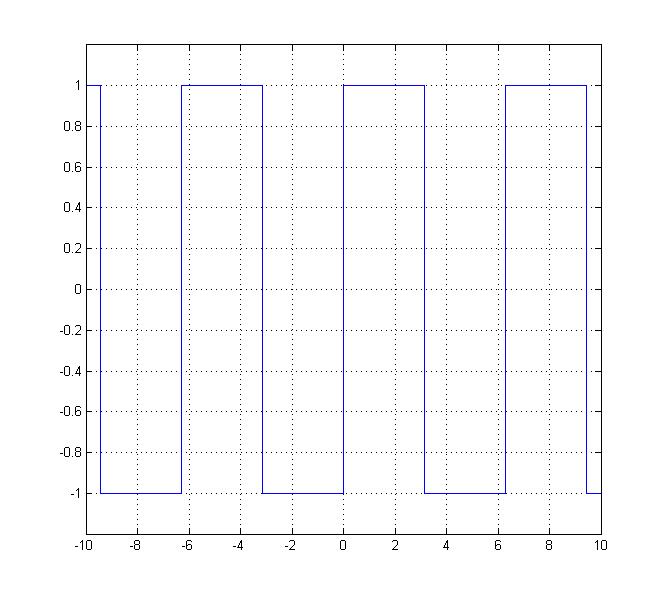
Given the following square wave $ \,x(t)\, $:
The function is periodic since there is a value $ \,T\, $ such that $ \,x(t+T)=x(t)\, $. In this example, the fundamental period is $ \,2\pi\, $, which one possible value for $ \,T\, $.
Non-Periodic Function: Decaying Square Wave
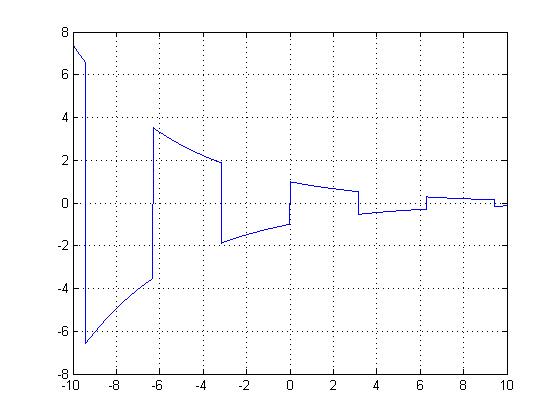
Given the following decaying square wave $ \,y(t)=x(t)e^{\frac{-t}{5}}\, $ ($ x(t) $ is the square wave defined in the previous section):
By inspection, this function is non-periodic, as there is no $ \,T\, $ such that $ \,y(t+T)=y(t)\, $. (The function is simply alternating between $ \,e^{\frac{-t}{5}}\, $ and $ \,-e^{\frac{-t}{5}}\, $ every $ \,\pi\, $ units, which neither are periodic.)