Periodic versus non-periodic functions (hw1, ECE301)

Read the instructor's comments here.

A periodic function is a function that repeats its values after some definite period has been added to its independent variable. This property is called periodicity.

For a function on the real numbers or on the integers, that means that the entire graph can be formed from copies of one particular portion, repeated at regular intervals. More explicitly, a function f is periodic with period P greater than zero if

f(x + P) = f(x) for all values of x in the domain of f. An aperiodic function (non-periodic function) is one that has no such period P (not to be confused with an antiperiodic function (below) for which f(x + P) = −f(x) for some P).

If a function f is periodic with period P, then for all x in the domain of f and all integers n,

f(x + nP) = f(x).

A plot of f(x) = sin(x) and g(x) = cos(x); both functions are periodic with period 2π.A simple example of a periodic function is the function f that gives the "fractional part" of its argument. Its period is 1. In particular,

f( 0.5 ) = f( 1.5 ) = f( 2.5 ) = ... = 0.5.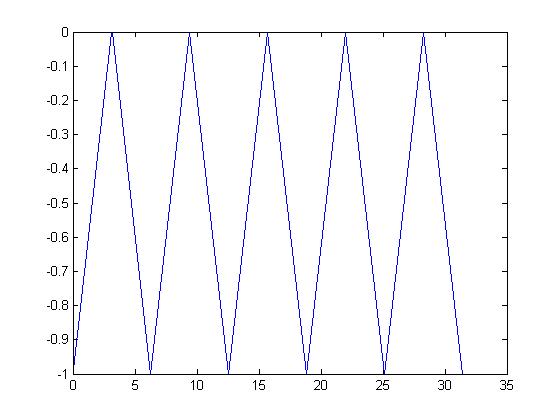

Non periodic signal is a signal that doesnt repeat its values after some definite period has been added to its independent variable.

Example of a non periodic signal.

q) Is cos(n) a periodic signal ?

we want a integer N such that cos (n+N) = cos (n) for all n

N is a multiple of 2*pi but since no integer multiple of 2*pi is an integer Therefore cos (n) is not periodic