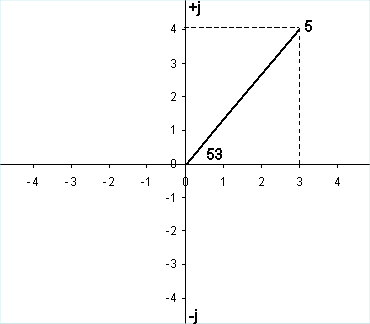== Complex Number Conversion ==
Recall that complex numbers use a plane similar to the X and Y coordinate system. In the complex system the X-axis is replaced by the Real axis and the Y-axis by the imaginary (j) axis. The imaginary axis is labeled "j" in the engineering world, while mathematicians usually use "i". This yields a coordinate system as below:
A phasor quantity can be expressed in one of two forms, polar or rectangular. Polar notation refers to the phasor using its' magnitude (length) and angle (direction). Rectangular notation refers to the phasor using its' real component and imaginary component.
Consider the phasor below,
In the polar form the phasor would be expressed as having a magnitude of 5 units at an angle of 53 degrees. In the rectangular form the same phasor would be expressed as having 3 units in the positive real direction and 4 units in the positive imaginary (+j) direction.
Converting between polar and rectangular form is a technique that will be used very frequently when dealing with reactive circuit analysis and you must be equally comfortable converting from polar to rectangular and converting from rectangular to polar.
Polar To Rectangular Conversion
When converting from polar to rectangular for the equations used are:
A couple of things to remember:
1. When entering theta use the value as measured from the positive real axis (0 degrees). The calculator will then give you the correct sign for the real and the imaginary components. 2. Be sure that your calculator is set to the angle units you are planning on using. If your problem is specified in degrees, make sure your calculator is set to degrees, not radians! 3. Remember to account for metric prefixes such as m, k etc.