Prerequisite Knowledge
This tutorial assumes you know what either the dot product or the inner product and what orthonormal bases are. A good review can be found HERE. First we will look at the 3 dimensional case over the real numbers like in MA265 , and then we will extend our understanding to the n-dimensional case over F like in MA351 or MA353. We will also take a look at these problems from a computational standpoint, as is done in CS314, to give light to the purpose behind QR-factorization.
Gram-Schmidt
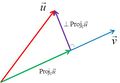
Projections
Let's say we have two vectors $ \vec{v_1} = \{ 3, 2, 0\}\quad and\quad\vec{v_2} = \{1, 2, 0\} $.
The Gram-Schmidt process is an algorithm by which we can orthogonalize a basis. The idea is the following.
Intuition
Let's say I've heard that the relationship between a person's height and their wingspan is approximately a 1:1 ratio. I'd like to test this theory and also come up with an equation that can estimate wingspan given a height. To get started, I've collected some sample data from a few of my friends.
| Height (in.) | Wingspan (in.) |
| 67.75 | 67.25 |
| 64.25 | 64.50 |
| 75.75 | 73.50 |
| 62.25 | 61.75 |
| 62.75 | 60.75 |
| 66.75 | 66.25 |
The first thing I'm going to do is plot my data on a graph and sketch a line that I think is a good estimate for my data. It will look something like this.